🍊 994.腐烂的橘子
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0 代表空单元格; - 值
1 代表新鲜橘子; - 值
2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
思路
基本思想
读完题之后,知道题目大致的流程是每一轮都是当前的橘子感染新的橘子,下一轮由新感染的橘子去继续感染得到更下一轮中的新感染橘子,相当于一个蔓延的过程,如果蔓延到最后,无法感染新橘子,还有新鲜橘子的话,返回-1,如果没有新鲜橘子的话,就返回感染了几轮
这样描述下来就是一个广度优先遍历的过程,也可以理解为树的层次遍历,但是树的层次遍历最开始只从一个根节点出发,这里相当于有多个"根节点",此时还是一样的逻辑,只是在"层次遍历之前",需要将所有的"根节点入队",增加了这样一步之后得到了多源广度优先遍历
需要注意的是,每次感染之后,需要将新鲜橘子的数量减一,并且这个新鲜橘子标记为被感染,入队之后下一轮从这些新感染的橘子出发进行蔓延

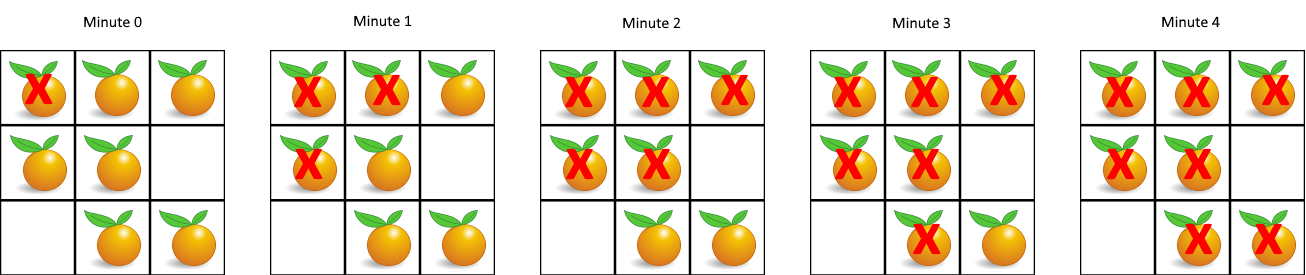
从图中可以看出,第一轮只蔓延了{[1,0],[0,1]}这两个橘子,第二轮从这两个新感染的橘子出发,感染了{[0,2],[1,1]}两个橘子,第三轮从这两个新感染的橘子出发,感染了{[2,1]}这个橘子,最后一轮感染了{[2,2]}这个橘子,至此所有的橘子都被感染完成,相当于没有新鲜橘子了,返回感染的轮次
执行流程
- 广度优先遍历之前增加一步,找到所有的"根节点"
- 按照广度优先遍历的方式,一层一层的遍历
- 统计遍历的层数
- 遍历到最后没有新鲜橘子或者无法感染新鲜橘子就返回结果
代码
根据以上描述,得出以下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
| class Solution {
public int orangesRotting(int[][] grid) {
LinkedList<int[]> queue=new LinkedList<>();
int flesh=0;
//找到所有"根节点"
for(int i=0;i<grid.length;++i){
for(int j=0;j<grid[0].length;++j){
if(grid[i][j]==1)
++flesh;
if(grid[i][j]==2){
int[] temp=new int[2];
temp[0]=i;
temp[1]=j;
queue.addLast(temp);
}
}
}
int res=0;
//广度优先遍历,查看多少层可以将橘子腐烂完
while(flesh>0&&!queue.isEmpty()){
++res;
int size=queue.size();
//每次从一层出发
for(int i=0;i<size;++i){
int[] temp=queue.removeFirst();
int x=temp[0];
int y=temp[1];
//腐烂上下左右的橘子,并且将腐烂后的橘子加入队列中
if(x>0&&x<grid.length&&grid[x-1][y]==1){
int[] up={x-1,y};
grid[x-1][y]=2;
queue.addLast(up);
--flesh;
}
if(x>=0&&x<grid.length-1&&grid[x+1][y]==1){
int[] down={x+1,y};
grid[x+1][y]=2;
queue.addLast(down);
--flesh;
}
if(y>0&&y<grid[0].length&&grid[x][y-1]==1){
int[] left={x,y-1};
grid[x][y-1]=2;
queue.addLast(left);
--flesh;
}
if(y>=0&&y<grid[0].length-1&&grid[x][y+1]==1){
int[] right={x,y+1};
grid[x][y+1]=2;
queue.addLast(right);
--flesh;
}
}
}
//遍历完之后还有新鲜橘子就返回-1,否则返回res
return flesh>0?-1:res;
}
}
|
总结
主要是从广度优先遍历出发,得到了多源广度优先遍历的方法,仅仅是在广度优先遍历的方法之前增加了一步找到所有"根节点"的步骤