968.监控二叉树

发表于： 分类于：
字数： 1811 阅读：≈ 4分钟

🌲968.监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例

示例 ：

  • 输入：[0,0,null,0,0]
  • 输出：1
  • 解释：如图所示，一台摄像头足以监控所有节点。

提示：

  1. 给定树的节点数的范围是 [1, 1000]。
  2. 每个节点的值都是 0。

思路

层次遍历

开始思路是层次遍历二叉树，然后看奇数层还是偶数层的节点少，将监控放在节点数少的层上即可，但是忽略了一点，能被监控到的节点不需要再进行监控，也就是隔一层监控一个不是最好的监控方案

所以需要三层一分组，一组中只需要中间的一层安装监控即可，不足三层的分成两种情况，所以一共有三种情况：

  1. level%3=0，此时只需要统计余3得2的层中有多少节点即可
  2. level%3=2，此时也只需要统计余3得2的层中有多少节点
  3. level%3=1，分开讨论，看奇数层和偶数层那个节点少

所以层次遍历的过程中需要统计层数和每一层的节点数

执行流程

  1. 执行层次遍历，统计二叉树的层数和每层的节点数
  2. 判断level%3的余数，从而分成两种（1，2可以合并成一种）情况
  3. 余数为2或者0，直接统计统计余3得2的层中有多少节点
  4. 余数为1，直接判断奇偶层中那个节点数少

但是这样只能通过一部分，情况模拟不全

后序遍历

基本思想就是孩子节点中有未被覆盖的，那么当前节点就需要装摄像头

如果孩子节点都被覆盖，那么就当前节点的父节点就需要装摄像头

如果孩子节点装了摄像头，那么当前节点就被覆盖

叶子节点不能被装摄像头，因为二叉树越底层节点越多，所以叶子节点不能装摄像头，尽可能地将摄像头向上装

一个节点有摄像头，上下两层都不用装。一个节点只是被覆盖，那么上层就需要被覆盖（自己装摄像头或者父亲装摄像头）

最后单独处理根节点，因为根节点可能自成一组

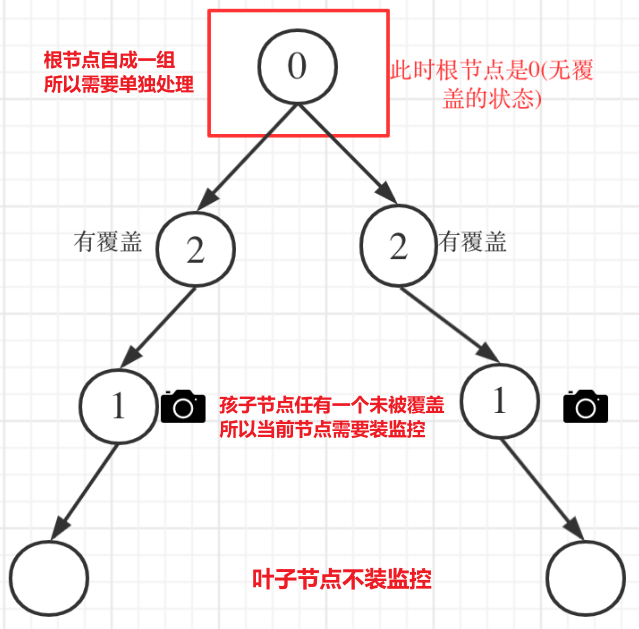
image-20230609195644650

执行流程

直接进行后序遍历，分成四种情况判断：

  1. 左右孩子都被覆盖，当前节点的父节点需要装摄像头
  2. 左右孩子任有一个为被覆盖，此时当前节点需要装摄像头
  3. 左右孩子任有一个有摄像头，当前节点被覆盖，父节点不用管它

注意2，3的顺序不能反，走到3默认两个孩子都被覆盖，就看是不是自带摄像头的覆盖

如果2，3顺序反过来，可能会出现一个孩子有摄像头，一个孩子不被覆盖，当前节点撒手不管的情况，因为当前节点没有排除任有一个为被覆盖，直接认为自己被覆盖，也就不会装摄像头

代码

层次遍历 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

class Solution {
public:
    int minCameraCover(TreeNode* root) {
        if(root==nullptr)
            return 0;
        if(root->left==nullptr&&root->right==nullptr)
            return 1;
        queue<TreeNode*> q;//使用一个队列层次遍历二叉树
        int level=0;//记录当前的层数
        vector<int> count;//统计每一层的节点数
        count.push_back(0);//让每层的节点数下标从1开始
        q.push(root);
        while(!q.empty()){
            int size=q.size();
            count.push_back(size);//统计一层的节点数
            //遍历一层节点
            for(int i=0;i<size;++i){
                //pop没有返回值，所以需要先front再pop
                TreeNode *node=q.front();
                q.pop();
                if(node->left!=nullptr){
                    q.push(node->left);
                }
                if(node->right!=nullptr){
                    q.push(node->right);
                }
            }
            ++level;
        }
        //遍历完二叉树之后，分情况讨论
        int res=0;
        int num=0;
        if(level%3==0||level%3==2){//看余3得2的层中有多少节点
            for(int i=1;i<count.size();++i){
                if(i%3==2){
                    res+=count[i];
                }
            }
        }
        if(level%3==1){
            for(int i=1;i<count.size();++i){
                if(i%2==0){
                    res+=count[i];
                }
                num+=count[i];
            }
            //判断奇偶层那个节点数少
            res=res<(num-res)?res:(num-res);
        }
        return res;
    }
};

后序遍历 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
private:
    int result;//全局变量统计监控数量
    int traversal(TreeNode* cur) {
        //为了让叶子节点不装摄像头，叶子节点的孩子节点默认被覆盖
        if (cur == NULL) return 2;
        int left = traversal(cur->left);    // 左
        int right = traversal(cur->right);  // 右
        //左右孩子都被覆盖，当前节点无法覆盖，其父节点装摄像头
        if (left == 2 && right == 2) return 0;
        //左右孩子任有一个无法被覆盖，此时当前阶段需要装摄像头
        if (left == 0 || right == 0) {
            result++;
            return 1;
        }
        //到这里就是左右孩子都被覆盖，就看是有摄像头的覆盖还是无摄像头的覆盖
        if (left == 1 || right == 1) return 2;
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        // 最后处理根节点
        if (traversal(root) == 0) { // root 无覆盖
            result++;
        }
        return result;
    }
};

总结

层序遍历模拟过程中总会丢掉一些情况，而题目的基本思想就是孩子节点中任有一个未被监控覆盖，当前节点就需要装摄像头，叶子节点属于孩子节点，所以不装摄像头，从下向上遍历模拟器来更方便，所以选择后序遍历，分为三种情况：

  1. 两个孩子节点都被监控覆盖，当前节点不用管他们，只需让自己的父节点装监控覆盖到自己即可
  2. 两个孩子节点任有一个未被覆盖，此时当前节点需要装监控才能覆盖到他们
  3. 两个孩子任有一个有监控，当前节点node可以被覆盖，node的父节点不用管它，只需管好自己

2，3的顺序不能调换