🌴96.不同的二叉搜索树

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例

1
2

输入：n = 3
输出：5

思路

基本思想

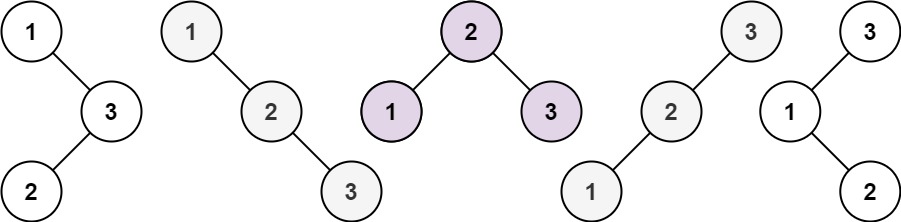
先从一个节点的树向后推导从而试图找出规律，可以发现n=3时，可以用1，2，3做根节点

以1做根节点时剩下两个节点全在右子树，两个节点的组合方式与n=2时的组合方式一样（不看节点上的值），以2做根节点时两个节点一左一右，组合方式与n=1的组合方式一样

所以节点数为n时形成的二叉搜索树最终搜索结果等于分别以1~n的节点为根节点，之后将序列分割成左右子树两部分之后，剩下的节点组成的结果

在代码中的的描述为：

1
2
3
4
5
6
7
8

//从前到后遍历最终形成n的结果
for (int i = 1; i <= n; i++) {
	//对于i个节点，分别与1~i作为根节点
    for (int j = 1; j <= i; j++) {
    	//将其分成左右子树两部分
        dp[i] += dp[j - 1] * dp[i - j];
    }
}

执行流程

从前到后遍历，为了最终统计n的结果提供参考

对于每个节点数i，都以1~i中的每一个节点作为根节点，从而将序列分割成左右两部分，最终节点数i的结果由所有的分割结果相加得到

最终遍历结束返回n的结果就是最终的答案

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
public:
    int numTrees(int n) {
        vector<int> res(n+1,0);
        res[0]=1;//初始化
        for(int i=1;i<=n;++i){
            for(int j=1;j<=i;++j){
                //以j为根节点从而将i分割成两部分
                res[i]+=res[j-1]*res[i-j];
            }
        }
        return res[n];
    }
};

总结

本题中从前向后遍历，后面的节点数形成的二叉搜索树利用了前面的节点数形成的二叉搜索树，只要两个二叉搜索树的结构一样，不管节点上的数是什么，都算做相同的二叉搜索树

例如节点23，24形成的二叉搜索树与2，3形成的二叉搜索树结构一样，所以可以直接作为n=2形成的二叉搜索树，明白这个道理之后，就可以得到动态规划方程

每个数都可以成为根节点，并且成为根节点之后会把序列分成左右子树两部分