➰️ 918.环形子数组的最大和

给定一个长度为 n 的环形整数数组 nums ，返回 nums 的非空 子数组 的最大可能和 。

环形数组 意味着数组的末端将会与开头相连呈环状。形式上， nums[i] 的下一个元素是 nums[(i + 1) % n] ， nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。

子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上，对于子数组 nums[i], nums[i + 1], ..., nums[j] ，不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。

思路

基本思想

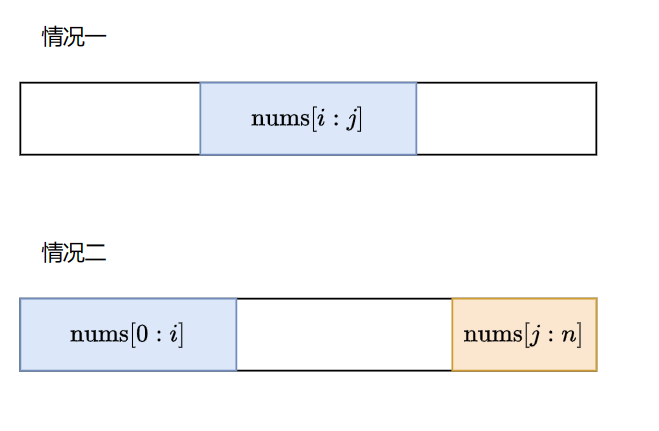
环形数组的最大子数组和就是可以在数组到了末尾时回到开头继续进行累加，只要被累加的元素没有被重复使用即可，由此可以看出，环形数组的最大子数组和有两种情况：

1. 正常的找到了最大子数组和，此时可以利用 53.最大子数组和 的解法求出最终的结果

2. 最大子数组和在尾部和头部各有一部分，此时使用逆向思维，求出最小子数组和，这个最小子数组和也可以利用 53.最大子数组和 的思想求出来，然后用数组的整体和减去这一个最小子数组和即可

   

针对 53.最大子数组和 来说，利用的是滑动窗口求出最终的答案，对比加上当前元素以及当前元素本身谁大，如果加上当前元素之后结果变小，说明前缀是小于零的数，此时结果变成当前元素，如果加上当前元素之后结果变大，说明前缀是大于零的数，此时可以进行累加，核心的判断逻辑就是：

1
2

maxPre=Math.max(maxPre+nums[i],nums[i]);
maxRes=Math.max(maxRes,maxPre);

在遍历的过程中不断更新最大值，利用这种思想，最小子数组和的求法就是将max换成min即可，最终需要注意的是，如果数组所有元素都是负数，那么求出的最大子数组和就是一个负数，此时最终返回的结果就是0和这个为负的最大子数组和，需要返回这个为负的最大子数组和

执行流程

1. 初始化最大辅助元素和最小辅助元素
2. 从头开始遍历，更新最大元素和最小元素
3. 遍历完成之后判断最大子数组和是否是负数，是的话代表数组中的元素全都是负数，此时直接返回
4. 如果不是全都是负数，那么就返回情况一和情况二中的最大值

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
    //分为两种情况：
    //1. 正常取值得到最大子数组和：直接计算即可
    //2. 两端取值得到最大子数组和：计算最小子数组和，用总和减去最小子数组和
    public int maxSubarraySumCircular(int[] nums) {
        int maxRes=nums[0],minRes=nums[0];
        int maxPre=nums[0],minPre=nums[0];
        int sum=nums[0];
        for(int i=1;i<nums.length;++i){
            //加了大一些还是不加大一些
            maxPre=Math.max(maxPre+nums[i],nums[i]);
            maxRes=Math.max(maxRes,maxPre);

            //加了小一些还是不加小一些
            minPre=Math.min(minPre+nums[i],nums[i]);
            minRes=Math.min(minRes,minPre);
            sum+=nums[i];
        }
        if(maxRes<0)
            return maxRes;
        else{
            return Math.max(maxRes,sum-minRes);
        }
    }
}

总结

主要将问题分成两种情况，然后针对第二种情况利用逆向思维求解，最大子数组和不好求，可以转而求最小子数组的和，只要出现了情况二，那么最小子数组和一定遍历一次就可以得到