909.蛇梯棋
🐍 909.蛇梯棋
给你一个大小为 n x n 的整数矩阵 board ,方格按从 1 到 n2 编号,编号遵循
转行交替方式
,从左下角开始 (即,从 board[n - 1][0] 开始)每一行交替方向。
玩家从棋盘上的方格 1 (总是在最后一行、第一列)开始出发。
每一回合,玩家需要从当前方格 curr 开始出发,按下述要求前进:
- 选定目标方格
next,目标方格的编号符合范围[curr + 1, min(curr + 6, n2)] - 该选择模拟了掷 六面体骰子 的情景,无论棋盘大小如何,玩家最多只能有 6 个目的地。
- 传送玩家:如果目标方格
next处存在蛇或梯子,那么玩家会传送到蛇或梯子的目的地。否则,玩家传送到目标方格next。 - 当玩家到达编号
n2的方格时,游戏结束。
r 行 c 列的棋盘,按前述方法编号,棋盘格中可能存在 “蛇” 或 “梯子”;如果 board[r][c] != -1,那个蛇或梯子的目的地将会是 board[r][c]。编号为 1 和 n2 的方格上没有蛇或梯子。
注意,玩家在每回合的前进过程中最多只能爬过蛇或梯子一次:就算目的地是另一条蛇或梯子的起点,玩家也 不能 继续移动。
- 举个例子,假设棋盘是
[[-1,4],[-1,3]],第一次移动,玩家的目标方格是2。那么这个玩家将会顺着梯子到达方格3,但 不能 顺着方格3上的梯子前往方格4。
返回达到编号为 n2 的方格所需的最少移动次数,如果不可能,则返回 -1。
示例
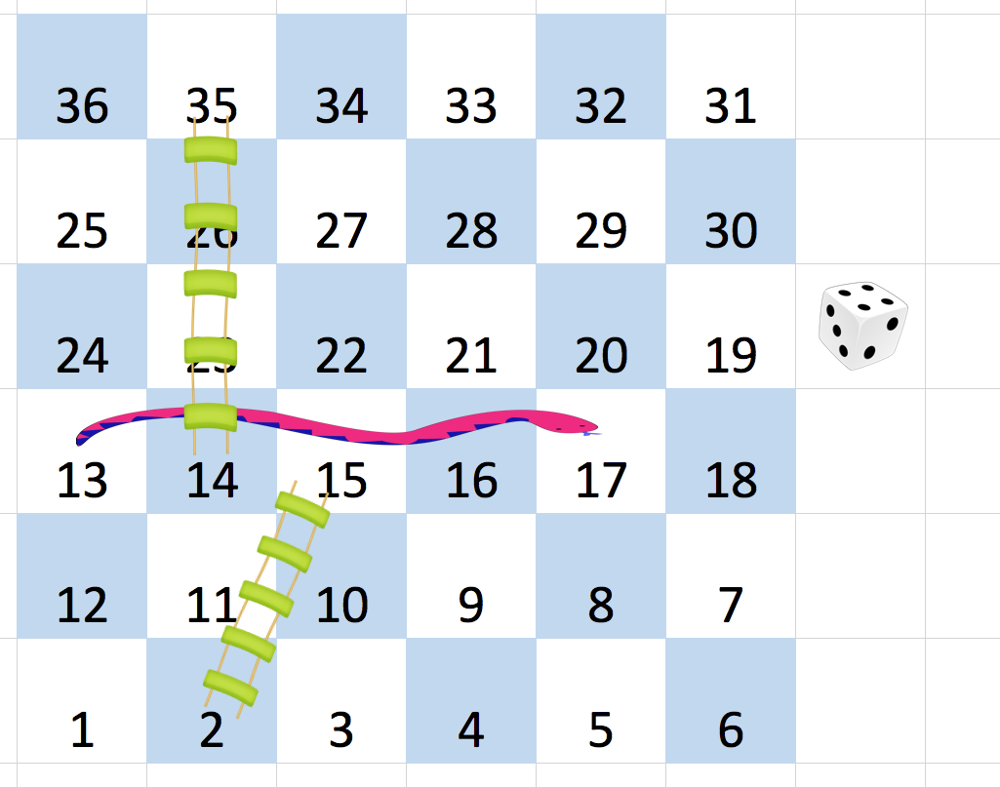
输入:board = [[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]] 输出:4 解释: 首先,从方格 1 [第 5 行,第 0 列] 开始。 先决定移动到方格 2 ,并必须爬过梯子移动到到方格 15 。 然后决定移动到方格 17 [第 3 行,第 4 列],必须爬过蛇到方格 13 。 接着决定移动到方格 14 ,且必须通过梯子移动到方格 35 。 最后决定移动到方格 36 , 游戏结束。 可以证明需要至少 4 次移动才能到达最后一个方格,所以答案是 4 。
思路
基本思想
蛇梯棋就是计算从1出发,最终到达n*n的位置需要的最短步长是多少,每走一步的步长为1,最长的距离就是从1一步一步的走到n*n,此时需要n*n步,但是在前进的过程中会遇到梯子或者蛇头,遇到梯子会前进,遇到蛇头会回退,这两个相互搭配之下,会形成一个最短路径,并且在这个基础上增加条件,步长可以为[1~6]中的任何数
此时可以将问题转换成图的广度优先遍历的问题,站在一个顶点上,只有六个孩子节点,每次都访问步长小的孩子节点,这样到达终点时就是所求的最短移动次数
需要注意的是,在遍历的过程中,路径上的数是成z字形交叉排列到一个矩阵中的,所以在前进的过程中需要注意计算出元素在矩阵中的真正出现位置,对于当前元素x来说,矩阵大小为n*n,正常从上到下排列时,行的位置是(x-1)/n,列的位置是(x-1)%n,如果元素是交叉排列,那么就用n-1再减去当前计算出来的行列位置即可
找到当前数值出现的行列位置时,需要判断行列位置处是否出现了蛇或者梯子(当前位置的数值大于0),只要出现了就到达指定的目的地
当前位置遍历完成,并且找到下一个数值出现的行列位置时,只要下一个数值没有被遍历过,就可以进行遍历,也就是可以加入队列中,然后继续遍历,针对每一个位置都尝试六种步长的前进方式,从小到大一旦找到了终点,就返回最终的答案
执行流程
- 初始化所有辅助数组,将起点加入队列中
- 从起点出发,依次从小到大尝试六种步长的前进方案
- 根据计算得到的数值得到当前数值应该出现的行列位置
- 判断行列位置是否到达终点,是否存在蛇或者梯子,然后进行一系列操作
- 如果当前位置没有被访问过,那么就将其加入待访问的队列中
- 重复上述步骤,直到到达终点或者结束循环
代码
根据以上分析,得出以下代码:
| |
总结
总结下来有两点,主要是问题的转换,将这个矩阵的遍历转换成了图的遍历,对于图中的每一个顶点都有六个孩子节点,并且每一个孩子节点在矩阵中的位置单独计算,经过这两点就解决了题目中的两个核心问题