👷 827.最大人工岛
给你一个大小为 n x n 二进制矩阵 grid 。最多 只能将一格 0 变成 1 。
返回执行此操作后,grid 中最大的岛屿面积是多少?
岛屿 由一组上、下、左、右四个方向相连的 1 形成。
思路
基本思想
为了形成最大人工岛,需要将临近的岛屿合并,合并的规则规定只能将一个海洋变成陆地,所以要尽可能的将临近的岛屿合并,但是找临近的岛屿不好找,于是换一种思路,找海洋的临近岛屿,如果一个海洋旁边(上下左右)有临近岛屿,就可以将岛屿合并,合并之后可能形成最大人岛,重点是合并的逻辑
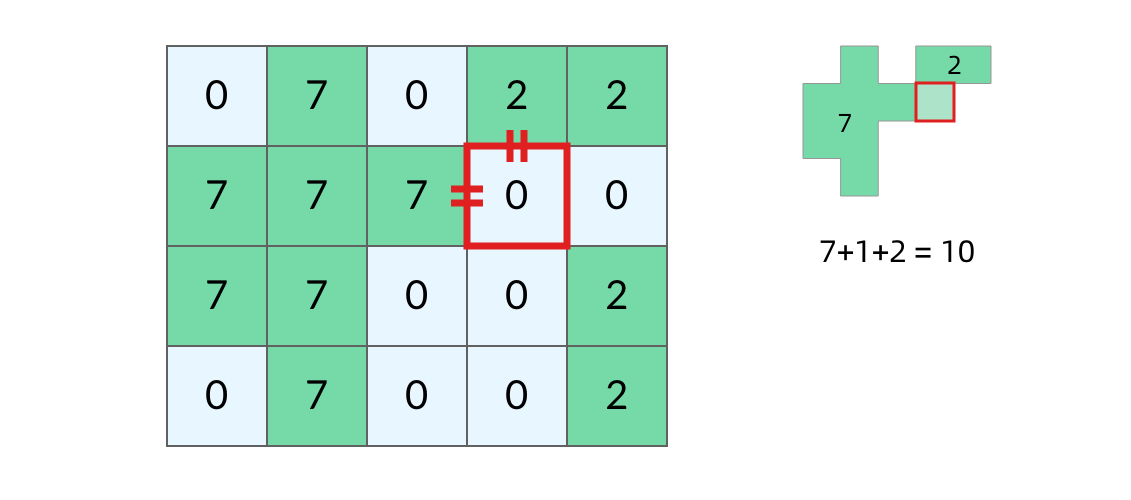
为了将岛屿合并,需要先计算各个岛屿的面积,计算之后,岛屿中每个陆地都需要进行标记,这样海洋找到了岛屿中的任何一个陆地都可以直接进行合并(面积的相加),所以这个标记需要记住岛屿的面积
如果直接使用面积做标记,那么出现海洋临近同一个岛屿的不同陆地时,就无法区分这两个陆地是来自同一个岛屿的两个陆地还是来自相同面积的两个不同岛屿中的陆地,所以需要使用一个map来记录面积和岛屿编号的映射,这样岛屿是唯一的,一旦海洋接壤一个不同的岛屿就可以通过map查询到面积,从而进行合并
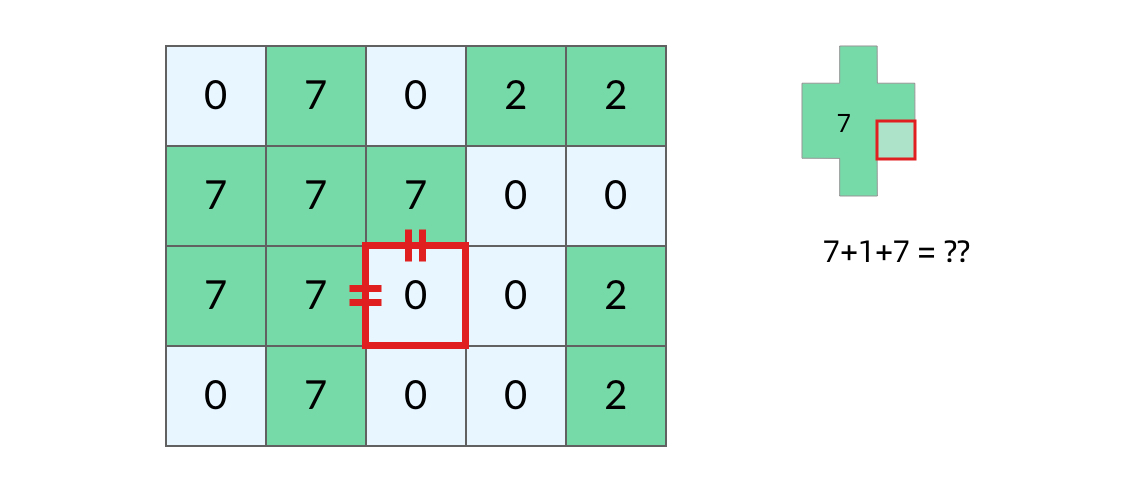
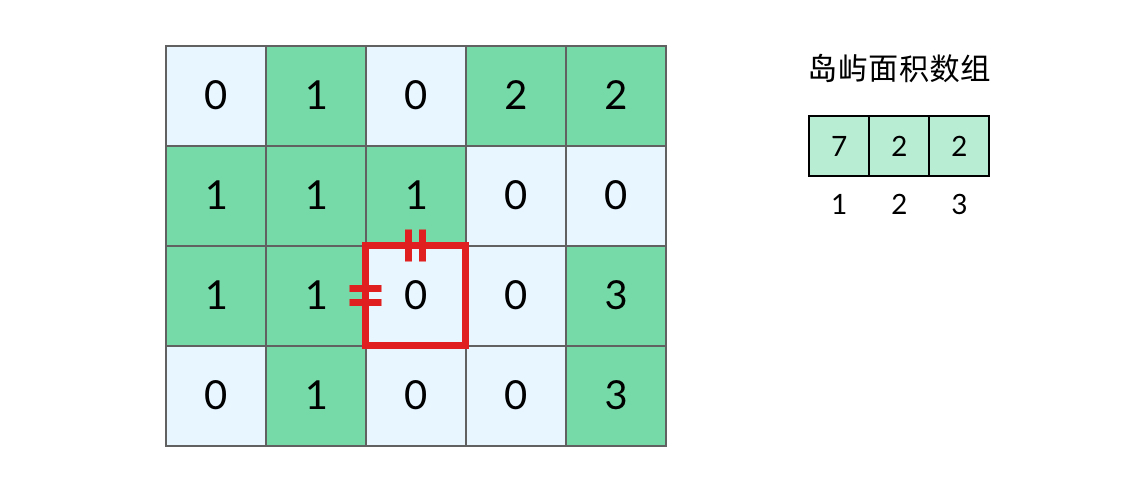
合并时可能出现好几种情况:上和左有不同岛屿,左和下有不同岛屿,下和右有不同岛屿,右和上有不同岛屿,上和左和下有不同岛屿,左和下和右有不同岛屿。。。甚至上下左右都有不同岛屿,所以还需要一个容器来记录那些岛屿被合并过
并且在初始求岛屿面积时,就需要记录最大岛屿的面积,最大岛屿的面积等于最大岛屿本身的面积加上可能存在的一个海洋,因为一旦给定的图中全是陆地,那么此时就不存在海洋,也就不需要合并,这样有两个好处:
- 当图中全是海洋时,求面积的循环不会执行,无法合并,此时最大陆地就是1,可以提前返回,结束代码
- 当图中全是陆地时,此时最大人工岛的面积就是最大岛屿的面积,并且不需要合并,此时可以直接返回最大的面积
剩下的就是普通的情况,需要先计算每个岛屿的面积,再看所有的海洋能不能将独立的岛屿进行合并
执行流程
定义求岛屿面积的函数,用来求岛屿的面积
按照常规的思想,求解每个岛屿的面积,并且将岛屿的面积和岛屿的编号进行映射,岛屿中遍历过的陆地全改成当前岛屿的编号,便于后期海洋合并时直接查询到这个岛屿的面积
注意岛屿的编号从2开始,避免出现未遍历的陆地原本编号是1,遍历过后岛屿的编号也是1,无法区分的问题
在求解岛屿面积的同时,记录当前最大的岛屿面积
求解完岛屿的面积之后,如果出现极端情况(全是海洋或者全是陆地),可以提前返回
遍历所有的海洋,一旦出现海洋的上下左右有岛屿,就可以尝试合并
为了防止岛屿重复合并(海洋的两侧是同一个岛屿)的问题,需要一个容器记录当前已合并的岛屿,从而可以防止重复合并
对于上下左右的方向,定义不同的合并代码
最终返回最大人工岛的面积
代码
根据以上分析,得出以下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
| class Solution {
public:
//如果当前两个岛屿之间只隔了一个海洋,那么当前两个岛屿就可以合并
int largestIsland(vector<vector<int>>& grid) {
//统计当前陆地的面积
//保存当前岛屿的索引与其面积的映射
unordered_map<int,int> umap;
//海洋的默认面积为1
umap[0]=1;
//index从2开始,防止与陆地初始的编号1冲突
int index=2;
//记录最大人工岛的面积
int res=0;
//岛屿的最大面积
int max_area=grid.size()*grid[0].size();
//统计岛屿的面积
for(int i=0;i<grid.size();++i){
for(int j=0;j<grid[0].size();++j){
if(grid[i][j]==1){
int area=0;
dfs(grid,i,j,index,area);
umap[index]=area;
//这里先更新,防止无法合并的情况
res=max(res,area+1<max_area?area+1:max_area);
index++;
}
}
}
//如果res==0,说明全是海洋,直接返回1
if(res==0)
return 1;
//如果res==max_area,说明全是陆地,不需要合并
if(res==max_area)
res max_area;
//看所有海洋的上下左右是不是岛屿,是的话连接起来是不是能构成最大人工岛
for(int i=0;i<grid.size();++i){
for(int j=0;j<grid[0].size();++j){
//遇到了海洋,查看上下所有是否有岛屿
if(grid[i][j]==0){
//上下左右任有一个位置有岛屿就可以更新
int area=0;
//用来临时保存已遍历过的岛屿
unordered_set<int> uset;
//没有越界并且海洋旁边出现了岛屿,岛屿没有统计过
if(i>0&&grid[i-1][j]&&
uset.find(grid[i-1][j])==uset.end()){
area+=umap[grid[i-1][j]];
uset.insert(grid[i-1][j]);
}
if(i<grid.size()-1&&grid[i+1][j]&&
uset.find(grid[i+1][j])==uset.end()){
area+=umap[grid[i+1][j]];
uset.insert(grid[i+1][j]);
}
if(j>0&&grid[i][j-1]&&
uset.find(grid[i][j-1])==uset.end()){
area+=umap[grid[i][j-1]];
uset.insert(grid[i][j-1]);
}
if(j<grid[0].size()-1&&grid[i][j+1]&&
uset.find(grid[i][j+1])==uset.end()){
area+=umap[grid[i][j+1]];
uset.insert(grid[i][j+1]);
}
//带上当前的海洋
area+=1;
res=max(res,area);
}
}
}
//当把所有的海洋遍历完毕之后,得到最终的最大人工岛面积
return res;
}
//统计面积的时候,将当前岛屿的陆地全部改成当前岛屿的索引
//一旦当前陆地有索引了,说明当前岛屿被遍历了
//并且index从2开始,防止与陆地初始的编号1冲突
void dfs(vector<vector<int>>& grid,int x,int y,int index,int &area){
if(x<0||y<0||x>=grid.size()||y>=grid[0].size()||
grid[x][y]==0||grid[x][y]==index)
return;
//当前陆地没有被遍历过,将当前陆地的值改成当前岛屿的索引代表当前位置被访问过
grid[x][y]=index;
area+=1;
//在当前陆地的上下左右遍历,计算当前岛屿的面积
dfs(grid,x-1,y,index,area);
dfs(grid,x+1,y,index,area);
dfs(grid,x,y-1,index,area);
dfs(grid,x,y+1,index,area);
}
};
|
总结
主要是岛屿合并的逻辑,合并时从海洋出发,一旦出现可以合并的岛屿,就可以尝试合并,合并时需要记住已合并的岛屿,为了合并需要建立岛屿和编号之间的映射,还有极端情况的处理也需要注意,合并时不能出现下标越界的情况


