🤏 77.组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

思路

基本思想

为了求出所有数的组合，最直接的办法就是for循环，当求两个数的组合时，只需要两层循环，求三个数的组合时需要三层循环，但是一旦组合个数过多，就会导致时间复杂度太高，并且由于组合个数是动态指定的，所以无法固定for循环的层数：

1
2
3
4
5
6

int n = 4;
for (int i = 1; i <= n; i++) {
    for (int j = i + 1; j <= n; j++) {
        cout << i << " " << j << endl;
    }
}

为了遍历所有的结果，可以采用回溯的办法，每一层都相当与一层for循环，但是采用递归的方式向下遍历，而不是强行for循环嵌套

当前一层遍历[1,n]的数，下一层遍历[2,n]的数，再下一层遍历[3,n]的数，以此类推，每层中选一个数，直接进行下一层的遍历，最后会形成一个搜索树

上一层选取一个数，可以跟下一层的所有元素配对，例如第一层先在[1,n]中选择一个1，这个1就可以和下一层[2,n]中的所有数依次配对，当形成一个个数为k的集合时，说明找到一个结果，此时将当前集合加入结果容器中，删除集合末尾的元素，重新建立新的集合，就这样一直搜索，最终可以搜索出所有的结果

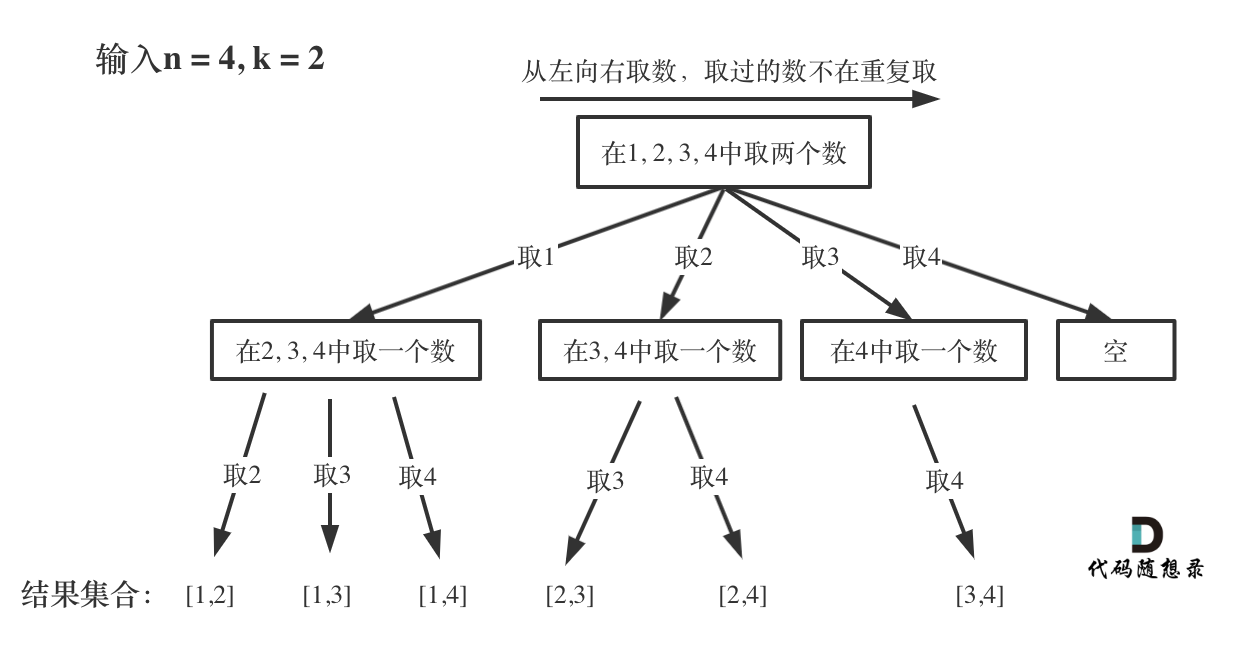
选择范围时可以进行优化，例如集合中共有5个元素，当前已选择3个元素，需要组成3个元素的集合，那么剩下的两个元素无法形成新的3的元素的组合，可以直接不遍历，新的搜索树为：

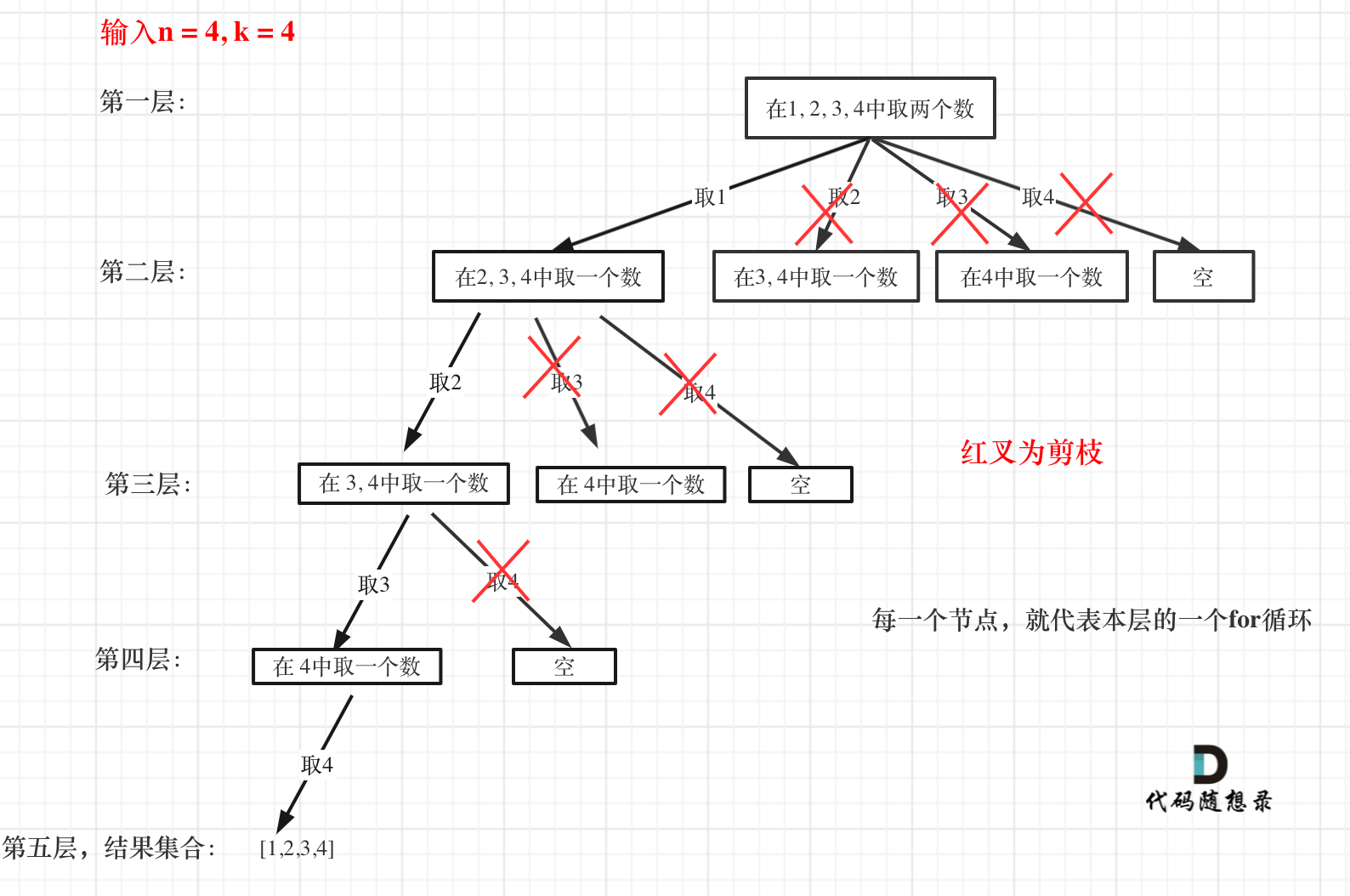
此时在代码中需要推导出i的变化范围，当集合中剩余元素大于等于所需要元素时，可以正常遍历，集合中的剩余元素可以用n-i表示，所需要的元素可以用k-path.size()来表示，所以只需要符合： $$ n-i>=k-path.size() $$ 也就是： $$ i<=n-(k-path.size())+1 $$ 之所以需要加1是因为容器元素的下标从0开始

如果题目要求元素可以重复选择的组合问题，那么下一层回溯的时候，元素的开始位置可以为i，而不是i+1，但是不能每次都从0开始，这样会导致之前遍历过的元素被重复选取，出现很多重复的组合

组合问题分为好几种：

1. 求所有元素的组合： 77.组合
2. 给定集合中元素不重复，并且不可以重复使用： 216.组合总和III ，此时就是搜索元素的幂集中哪些相加之后为目标值即可
3. 给定集合中元素不重复，但是可以重复使用： 39.组合总和 ，可以重复使用意味着下层遍历时可以从当前元素开始
4. 给定集合中元素重复，并且不可以重复使用： 40.组合总和II ，元素重复需要使用一个容器标记当前元素是否被使用，并且需要区分是同一层不能使用还是同一列不能使用，并且去重时为了让相同的元素相邻，需要对给定的元素进行排序

当给定集合中元素重复时，需要在当前层中去重，当元素可以重复使用时，下一层开始的下标可以与上一层相同，但是不能从0开始

执行流程

1. 判断当前遍历路径是否形成一个大小为k的集合，如果形成了，说明出现一个结果，将当前结果保留
2. 如果没有形成大小为k的集合，需要在下面的元素中搜索一个新的元素加入集合中
3. 当前元素x加入集合中，需要进行递归，在下一层中的[x+1,n]中找一个元素加入集合
4. 如果程序返回，说明形成一个符合要求的结合，此时删除集合最后的元素，加入一个新的元素，继续递归
5. 程序结果，结果容器中保存了正确的结果

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> combine(int n, int k) {
        backtrack(n,1,k);
        return res;
    }
    void backtrack(int n,int start,int k){
        //形成了一个k大小的集合
        if(path.size()==k){
            res.push_back(path);
            return;
        }
        //每次从一个元素出发，形成一个k大小的集合
        //for循环可以优化为
        for(int i=start;i<n-(k-path.size())+1;++i){
        //for(int i=start;i<=n;++i){
            //加入一个元素
            path.push_back(i);
            //递归
            backtrack(n,i+1,k);
            //进行回溯
            path.pop_back();
        }
    }
};

总结

主要是明白搜索的过程中会形成一个搜索树，搜索树分层，每一层的元素都会遍历与下一层的元素进行组合，从而形成不同的结果