647.回文子串

发表于： 分类于：
字数： 1124 阅读：≈ 3分钟

🔄647.回文子串

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例

  • 示例 1：

输入：s = “abc” 输出：3 解释：三个回文子串: “a”, “b”, “c”

  • 示例 2：

输入：s = “aaa” 输出：6 解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

两个aa不一样的原因是因为结束位置不同，但是为什么只有两个aa，应该有三个aa？

  • 提示：

    1. 1 <= s.length <= 1000
    2. s 由小写英文字母组成

思路

基本思想

需要求出字符串的全部子串，然后判断每一个子串是不是回文串，也就是求出当前字符串的幂集，然后统计幂集中的所有回文子串的数目，不包括空集

所以得到了一下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
public:
    vector<char> path;
    int res=0;
    int countSubstrings(string s) {
        backtrack(s,0);
        return res;
    }
    //回溯法求解字符串的幂集
    void backtrack(string s,int index){
        if(isCircle(path))//是回文串结果加一
            ++res;
        if(index==s.size())
            return;
        for(int i=index;i<s.size();++i){
            path.push_back(s[i]);
            backtrack(s,i+1);
            //回溯完成之后返回
            path.pop_back();
        }
    }
    //判断一个字符串是不是回文串
    bool isCircle(vector<char> s){
        if(s.size()==0)
            return false;
        for(int i=0,j=s.size()-1;i<j;++i,--j){
            if(s[i]!=s[j])
                return false;
        }
        return true;
    }
};

但是会出现问题，回溯法认为，aaa字符串会产生三个不同的aa，但是本题中认为只会产生两个不同的aa，按照题目要求确实应该产生三个不同的aa，不知道为什么。。。。

回溯法的办法行不通，于是考虑动态规划，此时动态规划由小到大的进行积累

其中dp[i][j]代表i~j区间的元素是否是回文串，可由更小的区间i+1~j-1确定，判断逻辑为：

1
2
3

if(s[i]==s[j]&&dp[i+1][j-1]){
    dp[i][j]=true;
}

当当前两个元素相等，并且更小范围的子串是回文串，那么当前子串也是回文串

由于当前的dp[i][j]由dp[i+1][j-1]确定，相当于新的元素由左下角的元素确定，所以遍历的时候需要从左下角开始遍历，对应到图中为：

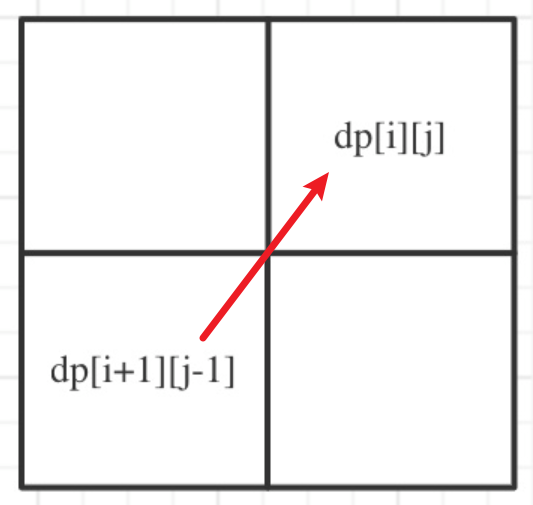
image-20230702200948694

判断回文时，有两种情况无法计算dp[i+1][j-1]

  1. i==j时，此时只有一个元素，所以一定是回文
  2. i+1==j时，此时有两个元素，在s[i]==s[j]的前提下，一定是回文串

这两种情况无法计算dp[i+1][j-1]，所以单独处理

执行流程

  1. 初始化dp数组
  2. 从左下角开始遍历
  3. 一旦你出现一个回文串，结果数就+1
  4. 返回最终结果

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
public:
    int countSubstrings(string s) {
        vector<vector<bool>> dp(s.size(),
                                vector<bool>(s.size(),false));
        int res=0;
        for(int i=s.size()-1;i>=0;--i){
            //为了从一个元素开始统计，j从i开始
            //搜索的范围就是主对角线的右半部分
            for(int j=i;j<s.size();++j){
                if(s[i]==s[j]){
                    //两种情况单独处理
                    if(i==j||i+1==j){
                        dp[i][j]=true;
                        res++;
                    }else if(dp[i+1][j-1]){
                        dp[i][j]=true;
                        res++;
                    }
                }
            }
        }
        return res;
    }
};

总结

主要是找到dp[i][j]和dp[i+1][j-1]的关系

并且知道需要从左下角开始遍历，内层循环的起始位置从i开始，这样可以保证先从一个元素的情况进行统计

并且知道当i==j或者i+1==j时，需要单独处理