😵 59.螺旋矩阵II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例
示例 1:

1
2
| 输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
|
示例 2:
思路
基本思想
为了模拟螺旋的情况,一圈循环当成一个整体,一圈一圈的向内收缩,并且每一圈可以分割成等长的四个长方形,分割情况如下图所示:
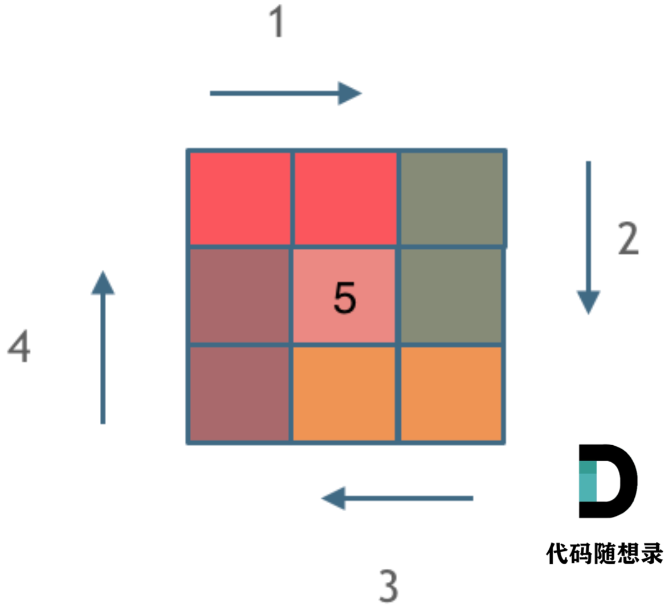
其中每一个颜色代表一个分割结果,创建螺旋数组时,需要选择一个起点,每一圈的起点都不同,并且每个螺旋数组旋转的圈数也不同,所以需要定义很多变量:
1
2
3
4
5
6
7
8
| int startx=0;//起点的横坐标
int starty=0;//起点的纵坐标
//由于每一圈的地点都在主对角线上,所以一个start就可以记录起点的位置
//int start=0;//起点的坐标
int loop=n/2;//螺旋数组遍历多少圈
int mid=n/2;//螺旋数组的中心点
int num=1;//螺旋数组中每个位置的值
int offset=1;//定义每一圈分割之后,长方形的长度
|
需要注意的是螺旋数组遍历多少圈,这个需要理解,如果给定n=3,那么只需要遍历一圈,如果给定n=5,那么需要遍历两圈
其中offset代表每一圈分割成四个长方体之后,长方体的长度,每遍历一圈,长方体的长度就会减小一,理解了这些就是纯代码模拟了
执行流程
- 从左到右填充第一个长方形,此时行不变
- 从上到下填充第二个长方形,此时列不变
- 从右到左填充第三个长方形,此时行不变
- 从下到上填充第四个长方形,此时列不变
- 一圈结束之后,更新下一圈的起点,并且下一圈的长方形的长度也需要更新
注意for循环中的i,j不能使用临时变量,要在for循环外定义,方便记住此时的遍历位置
代码
根据以上分析,得出以下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public:
//主要是靠代码模拟旋转
vector<vector<int>> generateMatrix(int n) {
int start=0;//起点的坐标
int loop=n/2;//螺旋数组遍历多少圈
int mid=n/2;//螺旋数组的中心点
int num=1;//螺旋数组中每个位置的值
int offset=1;//定义每一圈分割之后,长方形的长度
int i,j;
vector<vector<int>>res (n,vector<int>(n,0));
while(loop--){
//1. 从左到右填充,行不变
for(i=start;i<n-offset;++i){
res[start][i]=num++;
}
//2. 从上到下填充,列不变
for(j=start;j<n-offset;++j){
res[j][i]=num++;
}
//3. 从右到左填充,行不变
for(;i>start;--i){
res[j][i]=num++;
}
//4. 从下到上填充,列不变
for(;j>start;--j){
res[j][i]=num++;
}
//更新下一圈的起点以及下一圈中长方形的长度
start++;
offset++;
}
//如果给定的n是奇数,那么中心点单独处理
if(n%2==1){
res[mid][mid]=num;
}
return res;
}
};
|
总结
主要是将创建螺旋数组的步骤分成一圈一圈的,每一圈分割成四个大小一样的长方形,并且记录每一圈的起点和每一圈中长方形的长度,以此将问题分割,关键点总结为三个:
- 分割成以圈为单位
- 一圈分割成四个大小一样的长方形
- 记录每一圈的起点和长方形的长度

