🏃‍♂️55.跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例

示例 1:

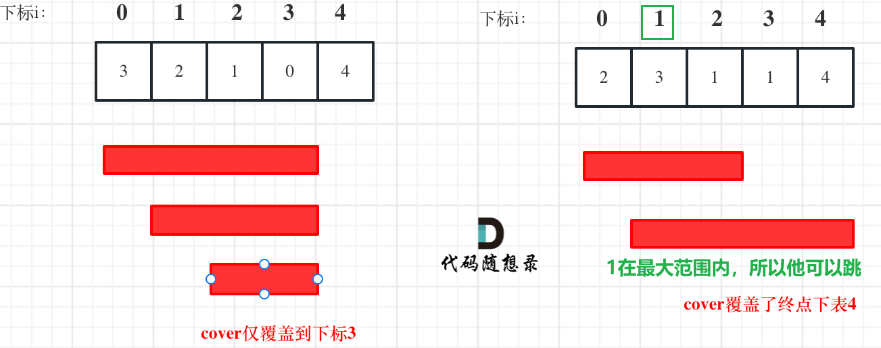
• 输入: [2,3,1,1,4]
• 输出: true
• 解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例 2:

• 输入: [3,2,1,0,4]
• 输出: false
• 解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

思路

基本想法

当前的元素代表的是跳跃的最大长度len，所以可以选择跳的长度范围为[0,len]，那么到了一个节点，选择跳几步呢

其实不管选择几步，都会有一个最大的范围，最大范围内的元素又可以跳，所以会越跳越远

重点就是最大范围内的元素可以跳，范围之外的元素不能跳，所以需要判断当前的元素是不是最大范围内的元素，也就是是不是可以由前面的元素跳到

相当于可以尽力跳出最远从而得出一个范围，范围之内的距离肯定都可以到达

执行流程

遍历容器，对于每一个元素，判断他是不是在最大范围内（第一个元素除外），如果是的话他就可以跳，一旦出现不在最大范围内的元素，后面的元素肯定都不在最大范围内，可以直接结束遍历

遍历结束后，判断最后一个下标是不是在最大范围内，是的话就可以跳到， 返回true，不是的话就不可达，返回false

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

class Solution {
public:
    bool canJump(vector<int>& nums) {
        //记录最大的范围
        int maxRange=nums[0];
        //直接从第一个元素开始
        for(int i=1;i<nums.size();++i){
            //在最大范围内就可以跳
            if(i<=maxRange){
                //更新maxRange
                maxRange=maxRange>i+nums[i]?maxRange:i+nums[i];
            }
            //出现元素在最大范围外跳不动了
            //或者已经可以到最后了
            if(i>maxRange || maxRange>=nums.size()-1){
                break;
            }
        }
        //判断是跳不动了还是到了最大的范围
        if(maxRange>=nums.size()-1)
            return true;
        else
            return false;
    }
};

总结

每个可达节点处都尽力而为，跳出最大的范围，如果终点在最大范围内，那么一定可达

如果出现某个节点不在最大范围内，说明这个节点不可达，剩下的节点也不可达（更远），所以停止跳跃，只有当节点在最大范围内是才可以继续跳跃