👑 52.N皇后II
n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
思路
基本思想
与
51题
思路一样,只是统计结果是略有不同,需要将问题分解,拆成两部分:
- 如何搜索整个棋盘,从每一个位置出发,遍历下面的棋盘都会形成不同的搜索结果
- 如何判断皇后之间不相互攻击,也就是同行同列同对角线都只有一个皇后
对于1来说,这种遍历所有情况的问题,使用回溯法最方便,每次选择一个新位置,然后就开始向下一层回溯,下一层遍历完成之后,返回上一层,继续选择下一个新位置,然后向下一层回溯,这样来来回回就可以搜索到所有的结果,形成的搜索树为:
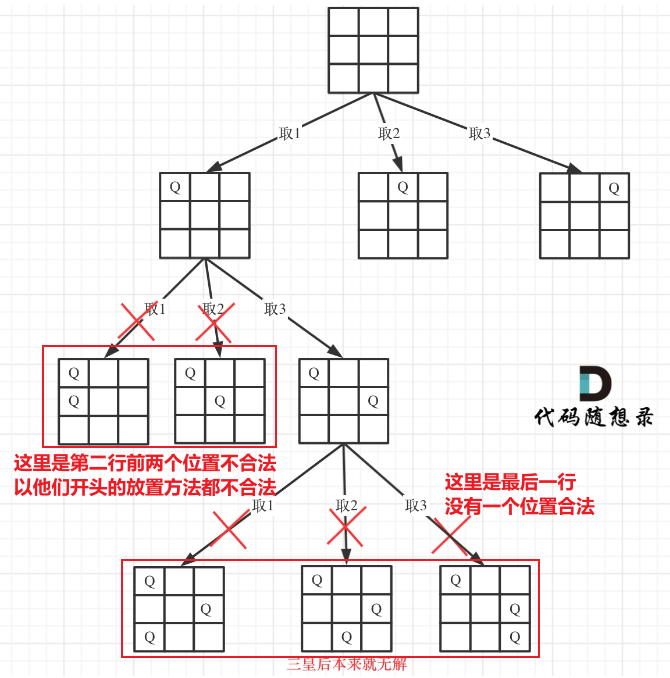
对于2来说,当前位置是否可以放皇后,取决于同列同对角线是否有皇后,同行一定没有皇后,因为当前行选中一个位置放皇后之后,会进入下一层,所以当前层在当前时刻只会存储一个皇后,下一层的位置经过合法性判断之后也可以放皇后
由于代码是从上到下遍历的,所以当前位置的西南方向和东南方向一定没有皇后,只需要判断当前列,东北方向,西北方向是否有元素即可
考的是代码模拟的能力,思路很简单
当遍历到最后一行的下一行时,说明所有行都放置了一个皇后,形成了一个方案,此时将这个方案统计,当回溯法结束,说明所有有效的方案都统计完毕
执行流程
- 回溯法遍历,穷举所有可能的情况
- 判断是否到了最后一行的下一行,也就是第n行,是的话说明形成了合法的结果,需要统计,不是的话转3
- 到了这里说明没有到最后一行的下一行,本行还需要放皇后,在本行中找一个有效位置,进入下一行继续找。。。
- 有效位置的判断有单独的函数
- 回溯法穷举结束,就可以统计出所有有效的情况
代码
根据以上分析,得出以下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| class Solution {
public:
int num=0;
int totalNQueens(int n) {
//1.判断当前位置是否可以放置皇后
//2.搜索出所有的结果
vector<string> chess(n,string(n,'.'));
backtrack(chess,0,n);
return num;
}
//判断当前位置是否合法
bool isValid(vector<string> chess,int row,int col,int n){
//看当前列是否有皇后
for(int i=0;i<row;++i){
if(chess[i][col]=='Q')
return false;
}
//看东北方向是否有皇后
for(int i=row-1,j=col+1;i>=0&&j<n;--i,++j){
if(chess[i][j]=='Q')
return false;
}
//看西北方向是否有皇后
for(int i=row-1,j=col-1;i>=0&&j>=0;--i,--j){
if(chess[i][j]=='Q')
return false;
}
//到这里都没有返回,说明此位置合法
return true;
}
//搜索所有结果
void backtrack(vector<string> chess,int row,int n){
if(row==n){//都走到最后一样的下一行了,说明形成了一个完整的棋盘
num++;
return;
}
//到这里说明没有形成完整的棋盘
//此时需要在这一行中选择一个合法的位置放置皇后
for(int i=0;i<n;++i){
//当前位置合法
if(isValid(chess,row,i,n)){
chess[row][i]='Q';
backtrack(chess,row+1,n);
//回溯
chess[row][i]='.';
}
//当前位置不合法,直接看下一位置是否合法
}
}
};
|
总结
学会如何将问题拆解,并且学会回溯法的
