😱51.N皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例 :
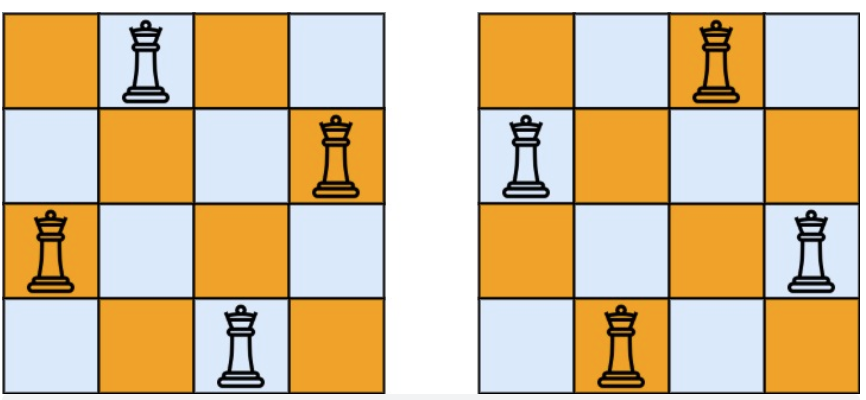
- 输入:n = 4
- 输出:[[".Q..","…Q",“Q…”,"..Q."],["..Q.",“Q…”,"…Q",".Q.."]]
- 解释:如上图所示,4 皇后问题存在两个不同的解法。
思想
基本想法
相当于一个n*n的二维数组,每当一个皇后占领一个位置,同行、同列和同斜线都不能再放皇后,主要问题我认为有两个:
- 如何求出所有可能:回溯法
- 如何判断皇后存在的行列位置不会引起冲突
回溯法解决以上问题,在一行中找到一个合法位置,然后再递归到下一行,再继续找,当递归到最后一行的下一行,说明找到一个完整的解法,此时加入结果集
至于如何判断皇后存在的行列位置不会引起冲突,直接分成三种情况,同列、同主对角线和同副对角线都没有皇后,那么当前位置就合法
为什么不用判断同行呢,因为递归的过程中一次只在一行中选一个位置就到了下一行,回溯的时候会进行回退再选择同一行中的下一个元素,所以行一定不会冲突
执行流程
首先定义一个棋盘用来放置元素,初始情况下一行有n个’.’,一共有n行
然后走到棋盘中的一个位置就判断一次,看是否合法,合法的话就将当前位置放上皇后,不合法的话就换一个位置
当形成一个合法的皇后,或者一行中没有一个元素合法走到for循环的末尾时,都会回溯,在回溯之前,每一行中的所有位置都会被判断,除非遇到半途而废的情况,直接回溯,后面几行直接不搜索,三皇后形成的搜索树如下:
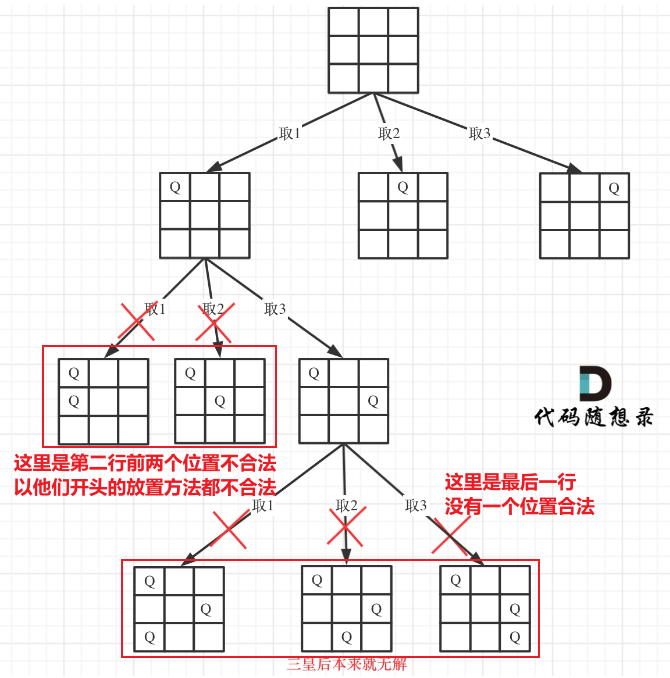
返回的情况不一样,有的半途而废,有的最后才发现不合法,有的最后满足条件加入结果集
判断当前位置是否合法只需要判断同列、同主对角线、同副对角线即可,因为递归每次只会在一行中选一个元素,并且回溯之后会手动回退,所以搜索判断的方向如图所示:
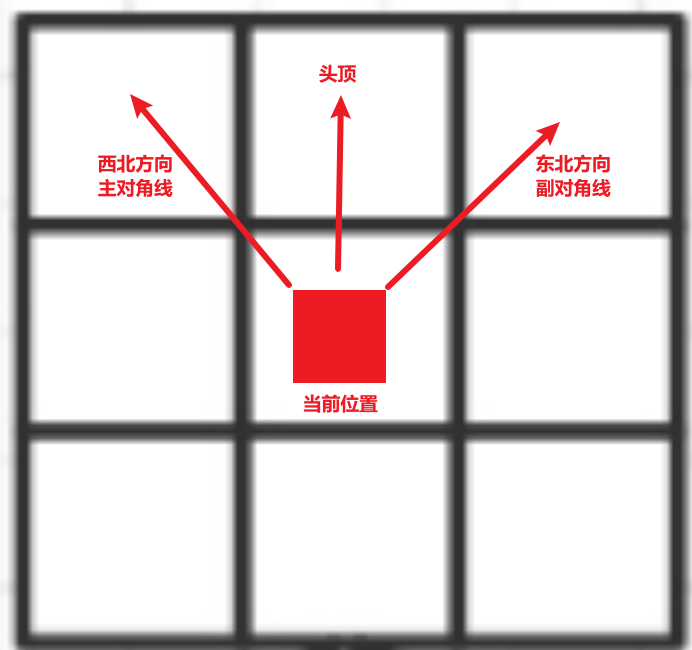
代码
根据以上分析,核心代码就是判断当前位置是否合法,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| class Solution {
public:
//使用全局变量存放结果
vector<vector<string>> res;
vector<vector<string>> solveNQueens(int n) {
vector<string> chessboard(n,string(n,'.'));
backtrack(n,0,chessboard);
return res;
}
//代码的核心,如何检查当前位置合法
//这里不能等于row和col,因为[row][col]是自己所在的位置
bool isValid(int n,vector<string>& chessboard,int row,int col){
//当前位置的同列有没有皇后
//当前位置的头顶有没有重复即可
for(int i=0;i<row;++i){
if(chessboard[i][col]=='Q')
return false;
}
//当前位置的同主对角线有没有皇后
//向西北移动
for(int i=row-1,j=col-1; i>=0&&j>=0; i--,j--){
if(chessboard[i][j]=='Q')
return false;
}
//当前位置的同副对角线有没有皇后
//向东北移动
for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++){
if(chessboard[i][j]=='Q')
return false;
}
//到这里都没返回,说明同列、同主对角线、同副对角线都不冲突
return true;
}
void backtrack(int n,int row,vector<string>& chessboard){
//最后一个元素都合法(n-1),才会走到n
if(row==n){
res.push_back(chessboard);
return;
}
//横向遍历,在一行中选择一个位置(列)
for(int i=0;i<n;++i){
//如果当前位置检查合法
if(isValid(n,chessboard,row,i)){
chessboard[row][i]='Q';
//在下一行找一个合法位置
backtrack(n,row+1,chessboard);
//到这里回溯
chessboard[row][i]='.';
}
//不合法当前位置放弃,找当前行的下一个位置
}
}
};
|
总结
使用回溯法的模板解决N皇后,重点就是如何判断当前位置合法
由于回溯法每次之选一行中的一个位置,所以同行一定不会冲突
同列判断只需要固定列,然后行从0移动到当前行的上一行,就是看当前位置的头顶有没有皇后即可
同主对角线判断也只需要看西北方向的头顶是不是有皇后即可,西北如何移动,从[row-1] [col-1]开始移动,行列都每次减一
同副对角线判断需要判断东北方向的头顶是不是有皇后,东北如何移动,从[row-1] [col+1]开始移动,行每次减一,列每次加一


