491.递增子序列

发表于： 分类于：
字数： 2011 阅读：≈ 5分钟

😴 491.递增子序列

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例

示例:

  • 输入: [4, 6, 7, 7]
  • 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:

  • 给定数组的长度不会超过15。
  • 数组中的整数范围是 [-100,100]。
  • 给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

自己的想法

思路

基本想法

是求数组幂集的改进，先求数组的幂集，然后将幂集中的所有递增子序列找出来，并且数组中的元素可能重复，所以需要进行两次判断：

  1. 递增子序列
  2. 元素没重复使用

形成新的搜索树：

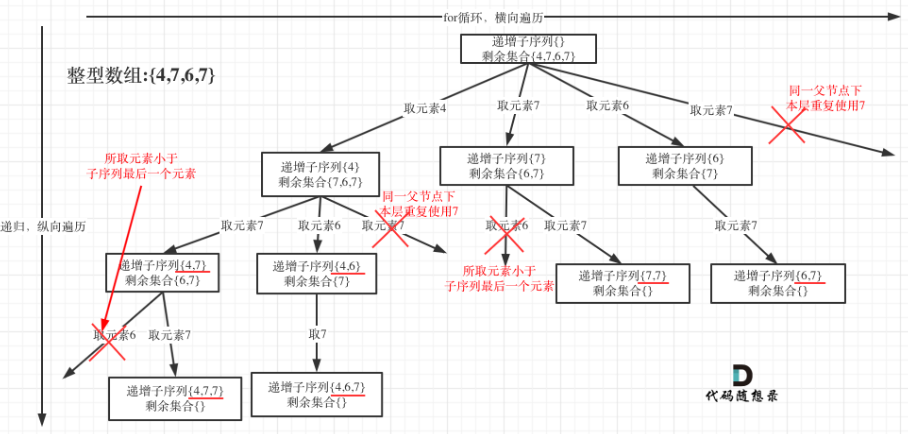
image-20230524200747307

执行流程

首先需要从头开始遍历，当子数组元素个数大于一才符合第一个要求，此时还需判断当前子数组中的元素是否是递增序列，最后还需判断数组中的元素是否重复使用。

并且由于求的是数组中自然递增的子序列，所以不能使用排序，不然所求结果就不是自然递增的子序列，判断元素重复的方法就不能简单的使用前一个元素等于当前元素，也就是：

1
2
3

if(i>index&&nums[i]==nums[i-1]){
	continue;
}

而是需要判断从index开始到当前位置的前一个元素有没有与当前元素重复的元素nums[index ~ i-1]==nums[i]??

总结来说，在求幂集的思路上，代码中还需要使用三个判断逻辑：

  1. 元素个数是否大于一
  2. 子数组是否是递增序列
  3. 是否使用重复元素

代码

根据以上分析，得出以下代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

class Solution {
public:
    //定义全局变量存放结果和子数组
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        if(nums.size()==0){
            return res;
        }
        backtrack(nums,0);
        return res;
    }
    //判断是否有元素与nums[i]重复,没有重复为false
    bool isSame(vector<int>& nums,int start,int end){
        //到这里肯定start!=end
        bool flag=false;
        //判断start~end-1范围内的元素是否与nums[end]重复
        for(int i=start;i<end;++i){
            if(nums[i]==nums[end])
                flag=true;
        }
        return flag;
    }
    void backtrack(vector<int>& nums,int index){
        //元素的个数大于一才判断是否是递增序列
        if(path.size()>1){
            //判断是否是递增序列，是递增序列为true
            bool flag=true;
            for(auto it=path.begin();it!=path.end()-1;++it){
                //不是递增序列
                if((*it)>(*(it+1))){
                    flag=false;
                }
            }
            //是递增叙序列才加入结果集
            if(flag){
                res.push_back(path);
            }
        }
        if(index==nums.size()){
            return;
        }
        //开始横向遍历
        for(int i=index;i<nums.size();++i){
            //判断nums[i]是否重复
            //使用了重复元素，当前元素不搜索，从下一元素开始搜索
            if(i>index&&isSame(nums,index,i)){
                continue;
            }
            //除了使用重复元素，其余的情况都符合要求
            else{
                path.push_back(nums[i]);
                //进行纵向遍历
                backtrack(nums,i+1);
                //触发任意一个返回条件进行回溯
                path.pop_back();
            }
        }
    }
};

出现的错误😢

编写代码时，出现两个错误：

  1. 判断是否是递增序列时，由于判断条件是(*it)>(*(it+1))，所以for循环的范围不再是

    auto it=path.begin();it!=path.end();++it，而是

    auto it=path.begin();it!=path.end()-1;++it，这样才不会访问到未知内存

  2. 判断是否使用重复元素时，判断的逻辑不应该是i>index并且没有重复元素时才进行递归，而是i>index并且出现重复元素就不进行递归，其余的情况都进行递归，否则会出现没有任何子集被选中的情况。

    也就是不应该使用代码：

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

    //使用了重复元素，当前元素不搜索，从下一元素开始搜索
if(i>index&&isSame(nums,index,i)){
	path.push_back(nums[i]);
	//进行纵向遍历
	backtrack(nums,i+1);
	//触发任意一个返回条件进行回溯
	path.pop_back();
}
//除了使用重复元素，其余的情况都符合要求
else{
	cotinue;
}

    而是使用：

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

    if(i>index&&isSame(nums,index,i)){
	continue;
}
	//除了使用重复元素，其余的情况都符合要求
else{
	path.push_back(nums[i]);
	//进行纵向遍历
	backtrack(nums,i+1);
	//触发任意一个返回条件进行回溯
	path.pop_back();
}

    代码随想录

    思路

    也是在子集的基础上进行筛选，但是使用的方法不同

    1. 判断是否时递增子序列的方法是在path进行push_back()之前判断将要加入容器的元素是否小于容器中最后一个元素，小于的话就不加入容器，这样可以保证元素每次加入容器之后，容器中的元素是非递减排列的

    2. 判断是否是重复元素使用了一个新的容器：unordered_set,相当于使用哈希表查找元素是否重复，一个元素一旦使用过，立刻将其加入哈希表中

    注意哈希表的建立时机，判断的是横向遍历时是否会使用重复元素，所以横向便利一开始就需要建立一个哈希表

    代码 

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

    class Solution {
public:
    //定义全局变量存放结果和子数组
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> findSubsequences(vector<int>& nums) {
        if(nums.size()==0){
            return res;
        }
        backtrack(nums,0);
        return res;
    }
    void backtrack(vector<int>& nums,int index){
        //当子数组元素个数大于一可以加入结果集
        if(path.size()>1)
            res.push_back(path);
        //进行横向遍历，定义一个哈希表判断元素是否重复
        unordered_set<int> Hash_Set;
        for(int i=index;i<nums.size();++i){
            //判断元素是否重复，是否是递增序列，不满足的continue
            if((!path.empty() && nums[i]<path.back())
                || Hash_Set.find(nums[i])!=Hash_Set.end()){
                    continue;
                }
            //到这里就既是递增序列又不是重复元素
            //正常进行回溯法三部曲即可
            path.push_back(nums[i]);
            backtrack(nums,i+1);
            path.pop_back();
            //注意！！，使用过的元素需要加入哈希表中
            Hash_Set.insert(nums[i]);
        }
    }

};

    总结

    对比自己的想法和代码随想录中的想法，都是将集合的幂集进行筛选，同时判断使用的不是重复元素，但是实现的方式不一样

    自己的想法时直接定义函数每次都需要调用函数判断是否是递增序列和是否使用重复元素

    代码随想录中直接在元素即将加入容器时就进行判断，每次都这样判断，可以保证容器中的元素一直都是非递减的，同时判断使用的是不是重复元素，二者结合进行筛选

    优化的部分个人觉得就是在判断子集合的递增上