46.全排列

发表于： 分类于：
字数： 999 阅读：≈ 2分钟

😍46.全排列

给定一个 没有重复数字的序列，返回其所有可能的全排列。

示例

示例:

  • 输入: [1,2,3]
  • 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

思路

基本想法

拿[1,2,3]举例，首先从1开始，先取2，再取3，形成[1,2,3]，之后取3，再去2，形成[1,3,2],

之后从2开始，取1，3形成[2,1,3]，取3，1形成[2,3,1]，最后从3开始，对剩下两个元素进行排列

总结来说就是取一个元素，再对剩下的元素进行全排列，依次取遍集合中的所有元素，剩下的元素全排列即可。

对于剩下的元素是一样的处理逻辑，从剩下的元素中取一个，依次取遍剩余集合中的所有元素，每次取一个剩下的元素，形成一个更小的集合。。。

由此形成一个搜索树：

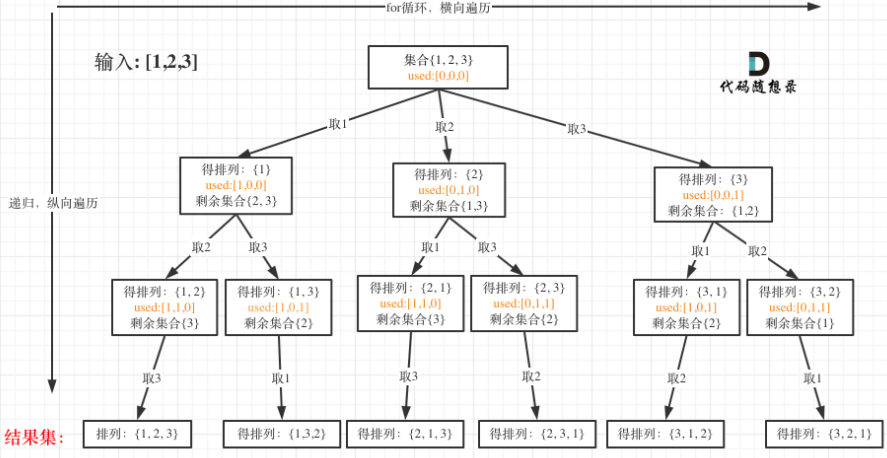
image-20230525185254477

相对于组合来说，排列可以每次都从头开始取元素，但是上层已经使用过的元素不能再用

执行流程

从之前的子集问题思路开始，确定递归结束的条件，for循环的范围

  1. 递归结束的条件：由于是全排列，所以当path中的元素个数等于nums中的元素个数时就形成了一个全排列，此时加入res结果集中并进行返回

  2. for循环的范围：由于每次取一个元素，再把剩下的元素进行全排列，所以不能简单的通过for循环的范围进行限制，而是需要使用一个标志记录当前哪个元素被使用

    并且由于需要进行多层递归，所以只能使用一个标志数组来记录每一层被使用过的元素

剩下的过程与子集问题完全一样

代码 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class Solution {
public:
    //全局变量存放结果和子集合
    vector<vector<int>> res;
    vector<int> path;
    vector<vector<int>> permute(vector<int>& nums) {
        if(nums.size()==0)
            return res;
        vector<bool> flag(nums.size(),false);
        backtrack(nums,flag);
        return res;
    }
    void backtrack(vector<int>& nums,vector<bool>& flag){
        //当形成一个排列时才加入res并返回
        if(path.size()==nums.size()){
            res.push_back(path);
            return;
        }
        //进行横向遍历，依次取一个元素
        for(int i=0;i<nums.size();++i){
            //当前元素没有在上一层和当前层被使用才进行全排列
            //flag数组中记录的是当前排列已经有哪些元素了
            if(flag[i]==false){
                path.push_back(nums[i]);
                //当前元素被使用，对应标志位变化
                flag[i]=true;
                backtrack(nums,flag);
                //回溯
                path.pop_back();
                //当前元素退出path，对应标志位也要变化
                flag[i]=false;
            }
            //当前元素被使用
            else{
                continue;
            }
        }
    }
};

总结

在子集的基础上放开限制，[1,2]和[2,1]在排列问题中是不一样的，在子集问题中是一样的，除了此处不同，在for循环判断条件上也有不同，子集问题有一个startIndex，而排列问题每次都是遍历整个集合，使用一个标志数组来记录哪些元素被使用过，所以在回溯时，不仅仅时path.pop_back(),还有flag[i]=false。

每一次从当前元素重新出发，但是需要注意的是，已经遍历过的元素不能再遍历了