455.分发饼干

发表于： 分类于：
字数： 951 阅读：≈ 2分钟

👶455.分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例

示例 1:

  • 输入: g = [1,2,3], s = [1,1]
  • 输出: 1 解释:你有三个孩子和两块小饼干，3 个孩子的胃口值分别是：1,2,3。虽然你有两块小饼干，由于他们的尺寸都是 1，你只能让胃口值是 1 的孩子满足。所以你应该输出 1。

示例 2:

  • 输入: g = [1,2], s = [1,2,3]
  • 输出: 2
  • 解释:你有两个孩子和三块小饼干，2 个孩子的胃口值分别是 1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2.

提示：

  • 1 <= g.length <= 3 * 10^4
  • 0 <= s.length <= 3 * 10^4
  • 1 <= g[i], s[j] <= 2^31 - 1

思路

基本想法

先将饼干的尺寸从大到小排序，再将孩子的胃口从大到小排序

然后依次取出一个饼干和一个孩子的胃口，匹配成功一此就将结果数加一

匹配到某一个地方饼干太小就找一个胃口更小的孩子，放在图中就是尺寸为9的饼干满足不了胃口为10的小孩，换一个胃口为7的小孩就好了

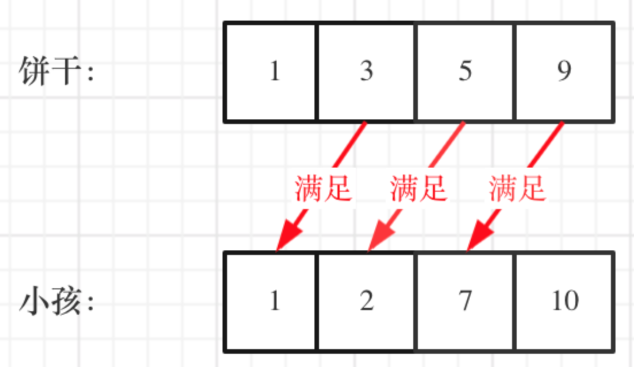
image-20230529201307367

当这个饼干的尺寸满足不了所有孩子的胃口，就说明程序结束

执行流程

按照上面的描述，有两个容器，需要先进性降序排序

然后进行匹配，匹配成功结果数加一，两个容器都向后移动

匹配失败只有孩子的胃口容器向后，当孩子的胃口容器遍历结束时直接返回结果集即可

代码

按照以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        //先将两个容器进行降序排序
        sort(g.begin(),g.end(),greater<int>());//胃口容器
        sort(s.begin(),s.end(),greater<int>());//饼干容器
        vector<int>::iterator git=g.begin();
        vector<int>::iterator sit=s.begin();
        int res=0;
        if(s.size()==0)
            return res;
        //饼干没了或者孩子分完了都算结束
        while(git != g.end()&& sit!= s.end()){
            //饼干尺寸大于等于胃口
            if((*sit)>=(*git)){
                ++sit;
                ++git;
                ++res;
            }
            //饼干尺寸满足不了孩子的胃口
            //换一个小胃口的孩子
            else{
                ++git;
            }
        }
        //统计结束返回人数
        return res;
    }
};

总结

先将容器排序，之后对于胃口大的孩子先分大尺寸的饼干，然后依次向下分

因为饼干尺寸降序，所以当前饼干无法满足当前的小孩时，就换一个胃口更小的小孩