💣452.用最少数量的箭引爆气球

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

示例

示例 1：

• 输入：points = [[10,16],[2,8],[1,6],[7,12]]
• 输出：2
• 解释：对于该样例，x = 6 可以射爆 [2,8],[1,6] 两个气球，以及 x = 11 射爆另外两个气球

示例 2：

• 输入：points = [[1,2],[3,4],[5,6],[7,8]]
• 输出：4

示例 3：

• 输入：points = [[1,2],[2,3],[3,4],[4,5]]
• 输出：2

示例 4：

• 输入：points = [[1,2]]
• 输出：1

示例 5：

• 输入：points = [[2,3],[2,3]]
• 输出：1

提示：

• 0 <= points.length <= 10^4
• points[i].length == 2
• -2^31 <= xstart < xend <= 2^31 - 1

思路

基本思想

只要气球所处的位置存在交集，就可以使用一只箭将其引爆，例如[10,16]和[7,12]存在交集[10,12]，所以这两个气球可以用同一只箭引爆，现在的目标就转换成了求气球之间的公共子集

也就是出现重叠的气球（有子集）就可以使用同一只箭将其引爆

为了尽可能（贪心）让气球挤在一起，这样就可以尽可能使用一只箭就将其引爆，所以做一个排序，

一旦出现没有交集，箭的数量就需要增加，并且这个位置就可以作为一个标志，用来与后面的气球进行比较看是否存在交集

执行流程

对容器进行排序，按照第一元素进行排序，让气球尽可能向左边靠，之后判断是否有交集

1. 以第一元素向后遍历，初始时使用一只箭，有交集就跳过

2. 没有交集箭的数量就要增加，同时以当前的气球为标志继续判断是不是有交集

3. 有交集还需要更新最小右边界，因为这样才能保证一只箭就可以引爆多个气球

   可以拿[10,16],[12,14],[15,18]举例，不更新最小右边界拿16比较的话，就会认为一只箭就可以

4. 重复2，直到遍历到容器末尾

只有边界重叠也算有交集，从而形成如下的遍历图：

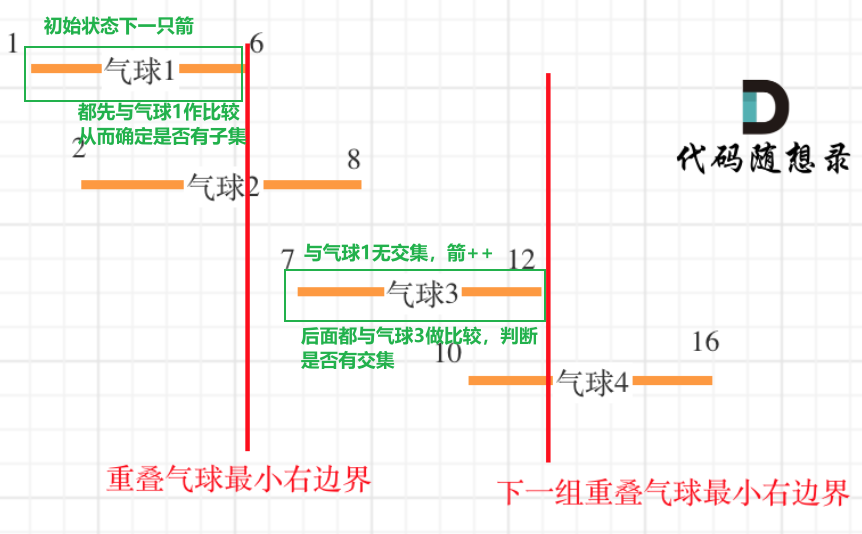
代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    public:
    int findMinArrowShots(vector<vector<int>>& points) {
        int arrow=1;
        sort(points.begin(),points.end(),[](vector<int>& v1,vector<int>& v2)		{return v1[0]<v2[0];}
         );
        //先排序再确定标志，不然就会记录排序之前的标志，从1开始就会出错
         vector<int> flag=points[0];
        //根据是否有交集统计箭的数量
        for(int i=1;i<points.size();++i){
            //没有交集
            //points[i][0]<=flag[1]都算有交集
            if(points[i][0]>flag[1]){
                ++arrow;
                flag=points[i];
            }
            //更新最小右边界,很重要！！！
            else{
                flag[1]=min(points[i][1],flag[1]);
            }
        }
        return arrow;
    }
};

总结

尽可能的将气球挤在一起，这样就能尽可能少的拿箭引爆，排序之后就求气球之间的交集，判断交集时边界重叠也算有交集。

但是[10,16],[12,14],[15,18]这种情况就是两个交集，需要使用两只箭，而不是一只，所以每次遍历都需要更新最小右边界

因为如果不更新最小右边界，[15,18]就会和[10,16]比较，就会认为有边界，其实[15,18]已经与[12,14]没有交集了，一只箭无法引爆他们两个，所以需要更新最小右边界

准备工作做完之后，在记录标志才符合要求