🚶‍♂️45.跳跃游戏II

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

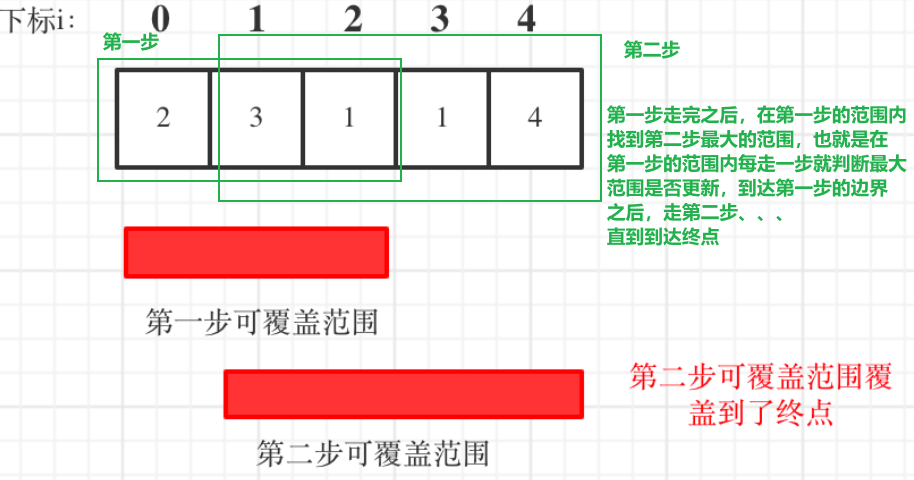
• 输入: [2,3,1,1,4]
• 输出: 2
• 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明: 假设你总是可以到达数组的最后一个位置

思路

基本思想

在跳跃游戏的基础上增加条件，要求最短的步数内到达终点，只需要遍历容器，遍历的过程中一旦出现最大范围到达或者超过终点就直接结束，简单修改条跳跃游戏的代码即可

但是需要注意什么之后才增加步数，每走一步都尽量是最大的一步

所以走第一步时有一个最大范围，在最大范围内的节点进行测试，看谁跳得最远，第一步范围内的节点测试完毕的标志是当前节点的下标就是最大范围，此时走一步，并更新最大范围，如果到达或者超过终点，直接结束

每一步的最大范围都尽可能的最大

执行

流程

每走一步都更新下一步的最大范围，第一步走完之后（节点到达第一步的最大范围），走第二步，在第二步的最大范围内更新第三步的最大范围、、、也就是说每一步都找下一步能到达的最大步数

就这样遍历，每一步都走最大的步数，当出现最大范围超过或者等于终点时，可以结束

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    int jump(vector<int>& nums) {
        if(nums.size()==1)
            return 0;
        int curRange=0;
        int nextRange=0;
        int step=0;
        for(int i=0;i<nums.size();++i){
            //每一步都尝试更新下一步的最大范围
            nextRange=nums[i]+i>nextRange?nums[i]+i:nextRange;
            //走到当前步的范围终点，选择最大的一步走出去
            //到了边界就走出下一步
            if(i==curRange){
                ++step;
                curRange=nextRange;
                if(curRange>=nums.size()-1){
                    break;
                }
            }
        }
        return step;
    }
};

总结

相比于跳跃游戏第一版本，只是判断终点是否可达，第二版本默认终点一定可达，只是要求解到达终点的最小步数，此时就需要尽量将每一步都走到最大

对于每一步来说，都有一个最大范围，先走第一步，在第一步的最大范围内找到能到达的最大范围，这就是第二步的最大范围，在第二步中找第三步。。。直到到达或者超越终点

可以看作是一个双层循环，外层循环走每一步，内存循环在每一步中找下一步的最大范围