37.解数独

发表于： 2023-05-28 分类于： leetcode

字数： 2208 阅读：≈ 5分钟

😯37.解数独

编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则：数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。空白格用 ‘.’ 表示。

示例：

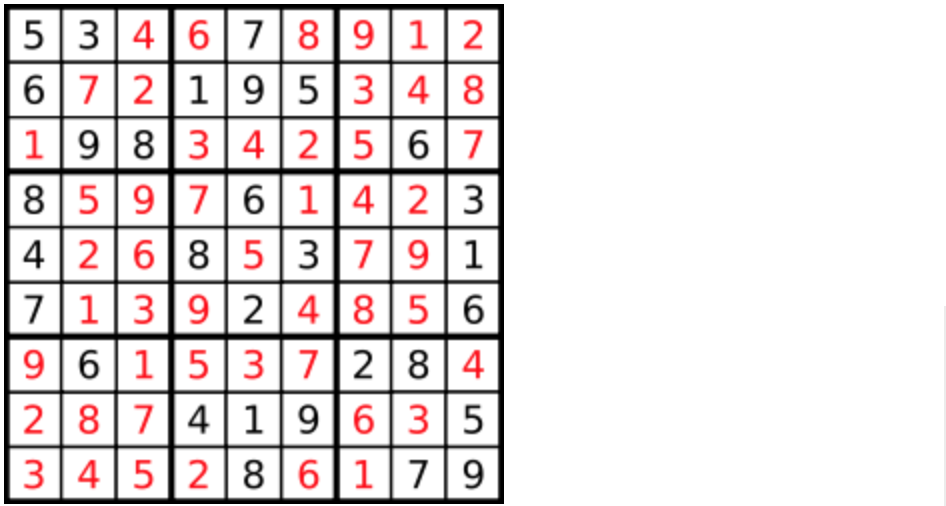
答案被标成红色。

提示：

给定的数独序列只包含数字 1-9 和字符 ‘.’ 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的

思路

基本想法

题目的要求是在每一个3 * 3的小空间中填充九个数字，每个3 * 3的小空间中本身就填充了一部分元素，只有’.‘的位置才需要填充元素

所以第一想法是使用回溯法，横向遍历取出一行中的一个空白位置，并且填入一个合法元素，之后再取出一行中的下一个空白位置填入一个合法元素，一行填充完成进行下一行，一旦遇到某一行冲突，就需要回溯一次，如果整个9 * 9的位置都被填满，说明找找到一个合法的数独，直接返回

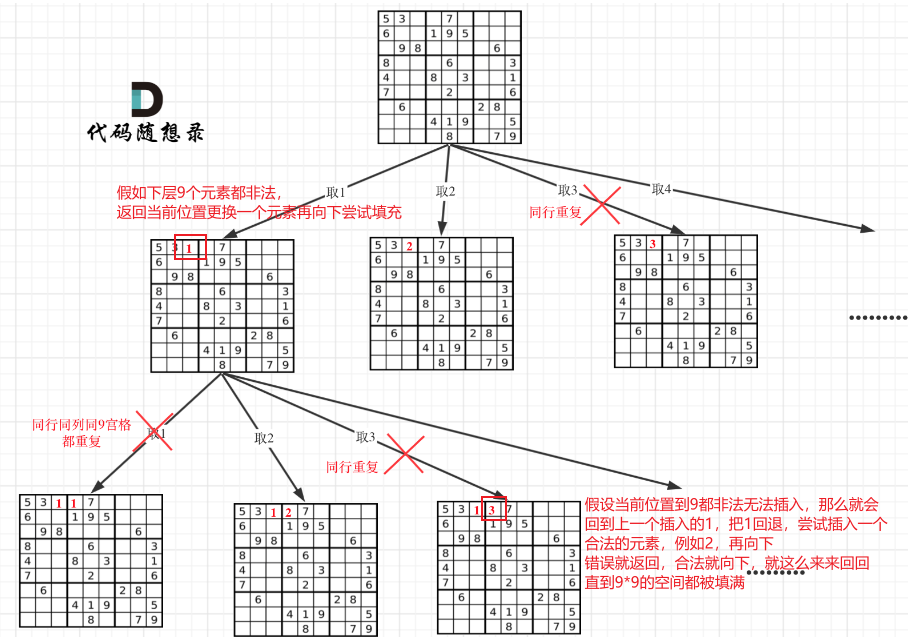
也就是从左到右，从上到下，依次填充每一个空白位置，遇到非法的情况就换一个数字填充，9个数字都非法就说明前面的位置填充出错，需要返回并回退，上层尝试下一个合法数字之后再向下递归

就像是尝试着向下，遇到错误向上修正，修正出错再向上

代码随想录中是每层都从[0] [0]的位置开始搜索一个空白位置，我认为可以记录上一层的行列位置，下一次从这个位置的下一个位置开始搜索即可，因为前面的位置都被填充了，完全可以从上一层的下一个位置开始，但是还没想明白为什么这样写程序会报错😕

记住当前位置的行，搜索时从当前行出发是可以的，但是不能记住当前位置的列，否则两层for循环就变成了：

1
2
for (int i = row; i < board.size(); i++) {        // 遍历行
        for (int j = col; j < board[0].size(); j++) { // 遍历列

假如当前行搜索完成都没找到空白位置，想从下一行开始找，按照上述for循环，就会直接从col开始，不会从0开始，会漏掉一些情况，但是记住但其当前位置的行是没错的，因为行搜索到末尾从下一行开始找时，行不会减小，但是列会，所以只能记住当前位置的行，但是这样也可以剪枝加快速度

举例来说：

如果我们记住当前2的位置，那么下一层搜索直接就从8开始了，就不会从6开始

执行流程

首先从[0] [0]开始找到一个空白位置，然后再从1-9中找到一个合法元素插入当前位置，进行递归

下一层递归也是从[0] [0]开始找到一个空白位置，之后找一个元素填充，

如何判断当前元素合法：

当前整行都没有重复
当前整列都没有重复
当前3 * 3方格没有重复

3 * 3方格中起点怎么算：

1
2
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;

如果遇到不合法的情况就需要向上返回

举例：

如果某层的某个位置9个元素都非法无法填充，那么就返回上层，在数独中就是上一个填充的位置，如果上一个填充的位置更换了9个元素下层还是非法，或者上一个填充的位置剩下的元素填进去自己非法，就说明上上层填充的有问题，进一步向上返回。就这么一层一层向上返回，每次返回一个小单位（向上一层，并换一个元素），直到9*9的位置都被填满，直接返回

根据以上分析，得出以下搜索树：

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
private:
bool backtracking(vector<vector<char>>& board) {
    for (int i = 0; i < board.size(); i++) {        // 遍历行
        for (int j = 0; j < board[0].size(); j++) { // 遍历列
            if (board[i][j] == '.') {
                // (i, j) 这个位置放k是否合适
                for (char k = '1'; k <= '9'; k++) {    
                    if (isValid(i, j, k, board)) {
                        board[i][j] = k;                // 放置k
                         // 如果找到合适一组立刻返回
                        if (backtracking(board)) return true; 
                        board[i][j] = '.';              // 回溯，撤销k
                    }
                }
                return false;  // 9个数都试完了，都不行，那么就返回false
            }
        }
    }
    return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
    for (int i = 0; i < 9; i++) { // 判断一整行里是否重复
        if (board[row][i] == val) {
            return false;
        }
    }
    for (int j = 0; j < 9; j++) { // 判断列里是否重复
        if (board[j][col] == val) {
            return false;
        }
    }
    int startRow = (row / 3) * 3;
    int startCol = (col / 3) * 3;
    for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
        for (int j = startCol; j < startCol + 3; j++) {
            if (board[i][j] == val ) {
                return false;
            }
        }
    }
    return true;
}
public:
    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board);
    }
};

对代码随想录的改进，记住当前位置的行，不用从头开始遍历,在13行增加一行代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
private:
bool backtracking(vector<vector<char>>& board,int row) {
    for (int i = row; i < board.size(); i++) {        // 遍历行
        for (int j = 0; j < board[0].size(); j++) { // 遍历列
            if (board[i][j] == '.') {
                // (i, j) 这个位置放k是否合适
                for (char k = '1'; k <= '9'; k++) {     
                    if (isValid(i, j, k, board)) {
                        board[i][j] = k;                // 放置k
                        //当前行遍历到最后一个元素，可以直接从下一行开始
                        //但是下一行必须从0开始
                        int rowTemp=(j==9?i+1:i);
                        // 如果找到合适一组立刻返回
                        if (backtracking(board,rowTemp)) return true; 
                        board[i][j] = '.';              // 回溯，撤销k
                    }
                }
                return false;  // 9个数都试完了，都不行，那么就返回false
            }
        }
    }
    return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
    for (int i = 0; i < 9; i++) { // 判断行里是否重复
        if (board[row][i] == val) {
            return false;
        }
    }
    for (int j = 0; j < 9; j++) { // 判断列里是否重复
        if (board[j][col] == val) {
            return false;
        }
    }
    int startRow = (row / 3) * 3;
    int startCol = (col / 3) * 3;
    for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
        for (int j = startCol; j < startCol + 3; j++) {
            if (board[i][j] == val ) {
                return false;
            }
        }
    }
    return true;
}
public:
    void solveSudoku(vector<vector<char>>& board) {
        backtracking(board,0);
    }
};

总结

每一层递归都从头开始找到一个空白位置尝试填充，合法就向下找到下一个空白位置继续填充，非法就返回上一层，更换一个填充元素再向下，如果无法填充就再向上，更换元素之后再向下，来来回回的进行递归回溯，直到9*9的位置都被填满。

其实每一层递归可以不从头开始，可以从当前位置的下一个位置开始，也就是记住当前位置的行，但是不能记住列，因为搜索下一行时需要从下一行的头开始，不能从col开始，否则会丢掉情况😄