🧤 31.下一个排列

整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。

• 例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

• 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
• 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
• 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须** 原地 **修改，只允许使用额外常数空间。

思路

基本思想

有点类似于贪心的思想，尽可能的修改给定数组的后面位置，这样才能找到下一个位置，修改的时候，需要找到一个合适的位置交换元素，这个合适的位置需要从后向前找，这样修改时修改的尽可能是低位，从而变化尽可能小，才能找到下一个排列

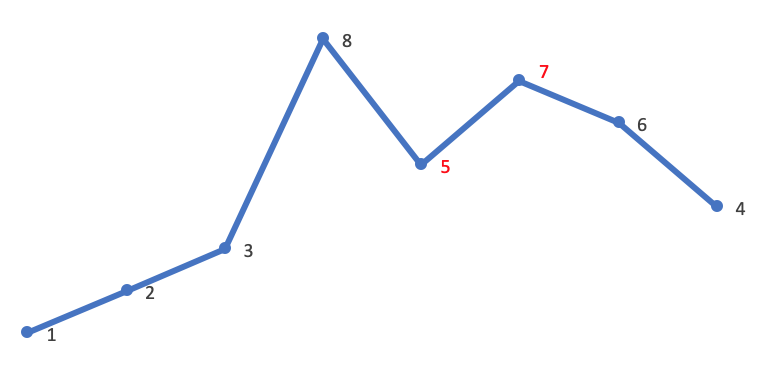
根据上面的分析，需要找到第一个可以交换的较小的数，所以第一步需要从后向前找到这个较小的数，所以需要从后向前找到第一个升序对，这个升序对的左边的元素就是可以替换的最小的数，对应到上图中就是[5,7]这个升序对，5就是可以替换的最小的数，将其替换就可以让整体变得稍微大一些

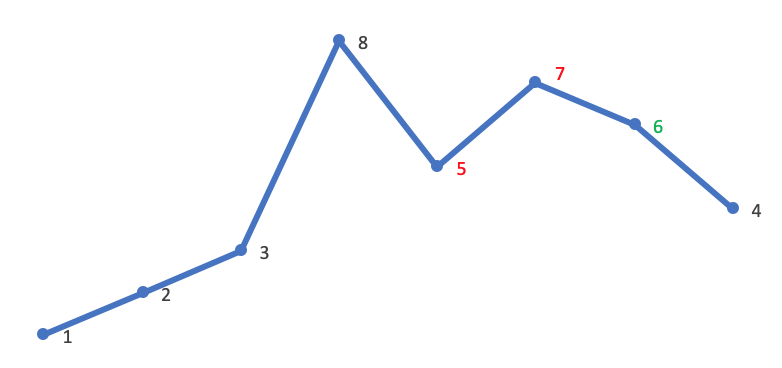
为了找到下一个排列，需要将这个最小的数替换为一个尽可能小的大数，也就是从后向前找出第一个比当前这个最小的数大的数，这个数是比这个最小的数大一点点的数，交换之后，可以让整体变大一点，对应到上图就是6,5和6交换之后，可以让整体变大，因为高位变大

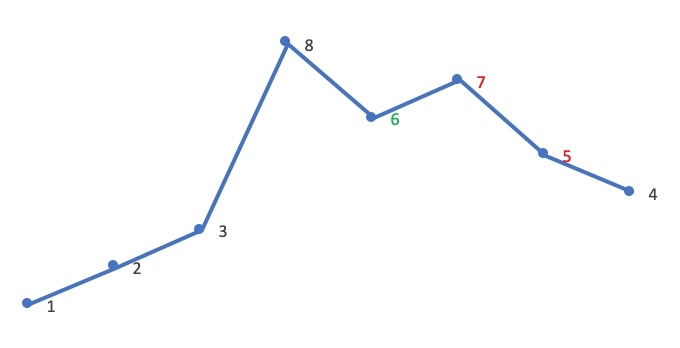
交换之后，需要注意的是，高位变大，后面的序列需要变的最小，从而使其成为下一个排列，为了让后面的序列变得最小，将其升序排列就变得最小，对应到上图就是5变成6之后，高位变大，后面的[7,5,4]还是降序，将其变得最小就可以让其变成下一个排列

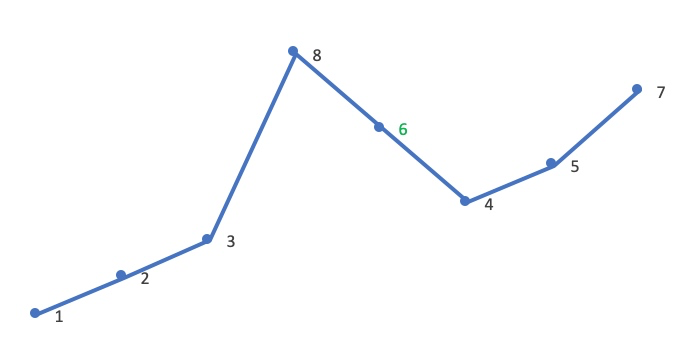
交换之后就形成了下一个排列，对应到下图中就是：

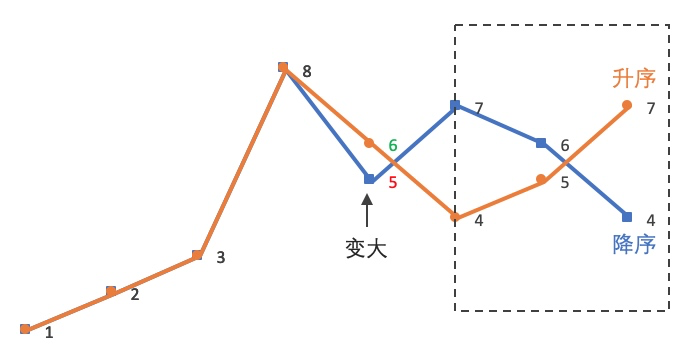
如果搜索下来没有发现一个升序对，那就是[3,2,1]的情况，根据题意，需要将字典重置为最小的排列，也就是将其升序排列即可，从[3,2,1]变成[1,2,3]直接逆序即可

执行流程

1. 从后向前 查找第一个 相邻升序 的元素对 (i,j)，满足 A[i] < A[j]。此时 [j,end) 必然是降序
2. .在 [j,end) 从后向前 查找第一个满足 A[i] < A[k] 的 k。A[i]、A[k] 分别就是上文所说的「小数」、「大数」
3. 将 A[i] 与 A[k] 交换
4. 可以断定这时 [j,end) 必然是降序，逆置 [j,end)，使其升序
5. 如果在步骤 1 找不到符合的相邻元素对，说明当前 [begin,end) 为一个降序顺序，则直接跳到步骤 4

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    public void nextPermutation(int[] nums) {
        int i=nums.length-2,j=nums.length-1,k=nums.length-1;
        //找到第一个升序对
        while(i>=0&&nums[i]>=nums[j]){
            i--;
            j--;
        }
        //从后向前找到第一个比nums[i]大的元素
        if(i>=0){//找到了就交换，没找到就是[3,2,1]的情况，直接逆序即可
            //在这里一定能找到
            while(nums[k]<=nums[i]){
                --k;
            }
            //交换，让nums[i]的位置变大一点
            int temp=nums[k];
            nums[k]=nums[i];
            nums[i]=temp;
        }
        //降序变成升序
        for(int left=i+1,right=nums.length-1;left<right;++left,--right){
            int temp=nums[left];
            nums[left]=nums[right];
            nums[right]=temp;
        }
    }
}

总结

类似于贪心的思想，尽可能找靠后的元素将其变大一点点，变大一点点之后，由于高位变大， 低位就可以变成最小，也不会影响整体变大，所以整体就是两步。第一步让尽可能靠后的高位变大，第二步让低位变得最小，经历两步之后就可以找到下一个排列