208.实现前缀树

发表于： 分类于：
字数： 1765 阅读：≈ 4分钟

🌴 208.实现前缀树

Trie （发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

  • Trie() 初始化前缀树对象。
  • void insert(String word) 向前缀树中插入字符串 word 。
  • boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
  • boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

思路

基本思想

前缀树也是一种树,只是树中的节点代表单词的一个字符,所以也称为字典树,每一个节点都有26个孩子节点,只是部分孩子节点才有值,由此形成了一个前缀树,也就是说,节点之间的连接完全可以使用一个数组来记录,26个元素的数组就可以记录节点之间的连接关系,对于单词cat来说,形成的前缀树如下:

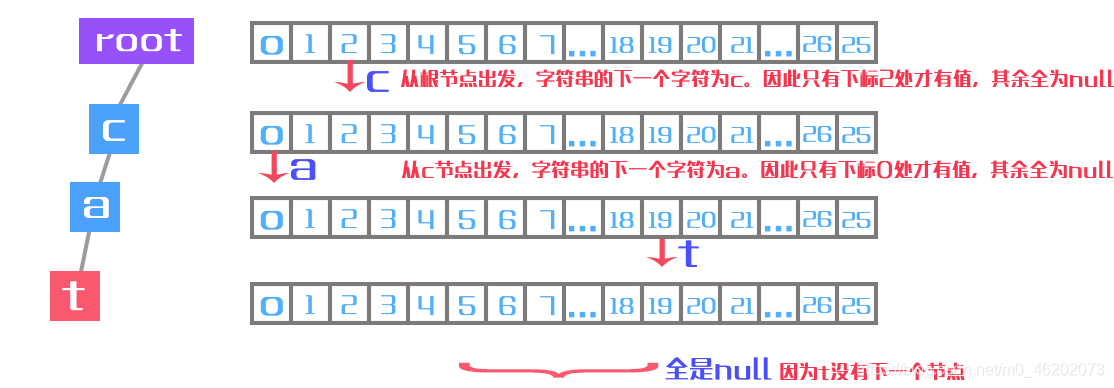
在这里插入图片描述

其中c的下一个字符是a,所以c对应的26个分支中,只有a这一个分支不为空,由于节点的下一个位置还是节点,所以存储下一位置的数组的类型就是节点的类型,这里可以类比链表的next指针的类型就是节点自身的类型

知道了前缀树的基本原理之后,就是形成前缀树了,每一个前缀树都有一个root根节点,根节点也有26个分支,所以在空的前缀树中插入一个单词可以从根节点出发,每次遍历单词中的一个字符,形成一个新节点,后续再插入单词时,部分字符有可能就不用插入了,因为部分单词的前缀相同,所以在前缀树中共用一部分树的节点,例如apple和app

所以插入时需要判断,例如插入a时需要判断,长度为26的数组的a字符所对应的位置是不是空,不是空就直接使用,是空需要创建新的节点,插入到这个位置,当单词插入完成之后,需要将单词的尾部做一个标记,说明这个单词已经到头了

核心就是节点之间的连接使用一个数组,数组的元素类型就是节点的类型

1
2
3
4

class TrieNode{
    public TrieNode[] children=new TrieNode[26];
    public boolean isEnd=false;
}

执行流程

  1. 对于插入单词来说,从根节点出发,每次截取单词中的一个字符,找到其在数组中的位置,在这个位置插入一个节点
  2. 插入节点之后,为了衔接下一个字符,需要有一个node节点一直指向当前已遍历的最后一个字符对应的位置上,以便新来的字符可以直接加入他的children数组中的某一个位置
  3. 单词遍历完成之后,node指向的是单词的最后一个字符,此时将这个字符标记为单词的末尾,代表单词结束

  1. 对于查找单词来说,从根节点开始,每次截取一个单词中的字符,判断这个字符对应的位置是不是有节点,有的话继续查询,没有的话直接返回

  2. 当前字符有节点,说明前缀树中存储了当前字符,此时查询单词中的下一个字符是不是存在于前缀树中,此时在前缀树中的匹配位置也需要移动,对应在代码中为:

    1
2
3
4

    if(node.children[index]==null)
	return false;
//在这里就是没有遇到,此时需要向后移动
node=node.children[index];

    也就是节点需要移动到下一个位置,跟随字符一起移动

  3. 判断到了单词的末尾,需要判断当前字符是不是结尾,不是的话也需要返回false,例如查找app,但是前缀树中只存储了apple,此时需要返回false,代表没有查到

代码

根据以上分析,得出以下代码:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

class Trie {
    private TrieNode root;
    //前缀树中的每一个节点都是一个前缀节点
    //包含一个26长度的节点数组和一个标记
    public Trie() {
        root=new TrieNode();
    }

    //插入时使用下标链接每个节点
    public void insert(String word) {
        //从头开始插入
        TrieNode node=root;
        for(int i=0;i<word.length();++i){
            int index=word.charAt(i)-'a';
            //当前前缀节点为空,说明没有创建,此时创建
            if(node.children[index]==null){
                //当前节点有了字符
                node.children[index]=new TrieNode();
            }
            //从这个字符继续添加
            node=node.children[index];
        }
        //单词添加完毕之后,最后一个字符的结尾标志需要点亮
        node.isEnd=true;
    }

    public boolean search(String word) {
        TrieNode node=root;
        for(int i=0;i<word.length();++i){
            int index=word.charAt(i)-'a';
            //查找过程中遇到了未添加的字符,直接返回false
            if(node.children[index]==null)
                return false;
            //在这里就是没有遇到,此时需要向后移动
            node=node.children[index];
        }
        //单词查找完了,看看是不是到了前缀树的末尾
        //防止出现apple和app的情况
        return node.isEnd;

    }

    public boolean startsWith(String prefix) {
        TrieNode node=root;
        for(int i=0;i<prefix.length();++i){
            int index=prefix.charAt(i)-'a';
            //查找过程中遇到了未添加的字符,直接返回false
            if(node.children[index]==null)
                return false;
            node=node.children[index];
        }
        //前一种是apple和app,后一种是app和app
        return !node.isEnd||node.isEnd;
    }
}
class TrieNode{
    public TrieNode[] children=new TrieNode[26];
    public boolean isEnd=false;
}

总结

主要是捋清楚前缀树相对于二叉树的不同,二叉树只有两个孩子节点,前缀树有26个孩子节点,而相同之处就是在于节点的连接上,next指针和children指针的类型都是节点本身的类型,这样才可以存储下一个节点是什么,从而链接成为一个树