🏝 200.岛屿数量
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
也就是一旦出现一个陆地,就需要将相邻(上下左右)的陆地全部统计出来,形成一座岛
思路
基本思想
核心思想就是每次找到一个岛,需要将岛中的所有陆地找出来,标记为遍历过,所以需要使用遍历的方法,遍历的方法与二叉树遍历的方法类似
二叉树遍历时,遇到叶节点需要返回,之后遍历当前节点的两个叶子结点,也可以理解为相邻的两个节点,转换到图的遍历中,超出图的边界需要返回,之后遍历当前节点的四个相邻节点,也就是上下左右的四个节点
在本题中,为了将所有的相邻陆地找出来,所以需要在遇到一个陆地时,需要一直向下遍历,将所有相邻陆地全部遍历一遍,这样才算是将一个岛屿找出来
返回的条件就是遇到了图的边界或者遇到了海洋,此时需要返回
一个陆地的所有相邻陆地全部遍历一遍,才能形成一个完整的岛屿
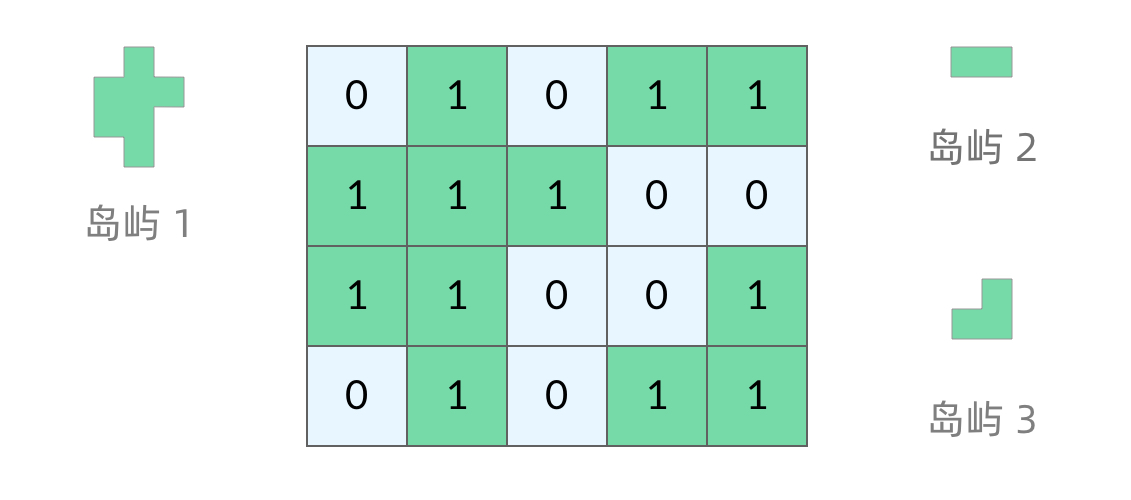
执行流程
- 遍历一个图
- 一旦遇到陆地节点,就需要将相邻的陆地全部找出来
- 遍历时出现已访问过的节点或者越界亦或是海洋节点时返回
- 当当前节点是陆地节点并且没有被访问过时,需要将当前节点标记为访问过,防止出现重复访问的情况
- 递归遍历当前节点的相邻节点(上下左右)
- 一个陆地的所有相邻陆地被访问过,一个岛屿才会形成
代码
根据以上分析,得出以下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public:
//什么时候才算是一个完整的岛屿
//将·所有陆地连接在一起,形成一个完整的岛屿
//也就是说,一旦遇到一个陆地,将与其相连的所有陆地统计出来,就可以形成一个岛屿
//统计完所有相邻的陆地,会形成一个岛屿
//再次遇到不相邻的陆地,就会形成新的岛屿
int numIslands(vector<vector<char>>& grid) {
int res=0;
for(int i=0;i<grid.size();++i){
for(int j=0;j<grid[0].size();++j){
//遇到没有遍历过的陆地,将相邻的所有陆地找出来形成一个岛屿
if(grid[i][j]=='1'){
dfs(grid,i,j);
//岛屿数量+1
++res;
}
}
}
//返回最终的结果
return res;
}
void dfs(vector<vector<char>>& grid,int x,int y){
if(x<0||y<0||x>=grid.size()||y>=grid[0].size()|| //超过图的边界
grid[x][y]=='0'|| //遇到了海洋
grid[x][y]=='2') //遇到了遍历过的节点
return;
//到这里说明当前位置没有超过边界,也不是海洋,也没有遍历过
grid[x][y]='2';
//遍历四周相邻节点
dfs(grid,x-1,y); //上
dfs(grid,x+1,y); //下
dfs(grid,x,y-1); //左
dfs(grid,x,y+1); //右
}
};
|
总结
核心就是如何遍历图,参考二叉树的遍历逻辑,并且岛屿形成的标志是所有相邻的陆地全部被访问过后,才能形成完整的岛屿
