142.环形链表II

发表于： 分类于：
字数： 1058 阅读：≈ 3分钟

➰ 142.环形链表II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

思路

基本思想

相比于 141题 ，本题不仅需要判断是否有环，还需要将入环的第一个节点给找到，所以增加了难度，在141题的基础上，如果有环，需要增加代码，将入环节点找到

此时有两种解决办法，第一种直接抛弃141题的方式，遍历链表，将链表存储到一个unordered_set中，一旦存储的过程中发现容器中有了此节点，说明找到了第一个入环节点，此方式需要使用容器辅助，增加了空间复杂度

第二周解决办法就是在141题的基础上，通过推导发现数学规律，从而找到入环节点，当找到环时，快慢指针所处的状态如图所示：

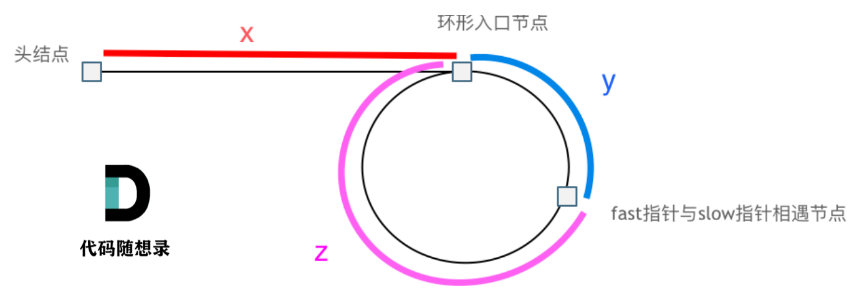
image-20230725191412350

此时slow指针走过的步数为x+y，fast指针走过的步数为x+y+n(y+z)，并且由于快指针走两步慢指针才走一步，所以两个指针步数之间的关系为： $$ x+y+n(y+z)=2(x+y) $$ 化简之后为： $$ n(y+z)=x+y $$ 进一步化简为： $$ (n-1)(y+z)+z=x $$ 也就是说，x和z之间，就差了若干个y+z，从快慢指针相遇节点和头结点分别出发，再次相遇的节点就是入环节点

执行流程

方法一

  1. 定义一个unordered_set
  2. 遍历链表，尝试将每一个节点加入容器
  3. 加入之前判断容器中是否已存在当前节点
  4. 已存在直接返回当前节点，不存在继续遍历
  5. 遍历到结束都没有找到就返回nullptr

方法二

  1. 快慢指针从头出发
  2. 快指针走两步慢指针走一步
  3. 当快慢指针相遇时有环
  4. 从快慢指针和头结点的位置分别出发向后遍历
  5. 第一个相遇位置就是入环节点
  6. 没找到环返回nullptr

代码

根据以上分析，得出以下代码：

方法一 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head==nullptr)
            return head;
        unordered_set<ListNode*> uset;
        ListNode* node=head;
        while(node!=nullptr){
            //不是入环节点，加入容器
            if(uset.find(node)==uset.end()){
                uset.insert(node);
                node=node->next;
            }else{//找到入环节点直接返回
                return node;
            }
        }
        return nullptr;
    }
};

方法二 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head==nullptr)
            return head;
        ListNode* fast=head;
        ListNode* slow=head;
        while(fast!=nullptr&& fast->next!=nullptr){
            fast=fast->next->next;
            slow=slow->next;
            if(slow==fast){//有环，需要找到入环节点
                //从快慢指针相遇节点和头结点分别出发
                //第一次相遇的节点就是入环节点
                ListNode* n1=head;
                ListNode* n2=fast;
                while(n1!=n2){
                    n1=n1->next;
                    n2=n2->next;
                }
                return n1;
            }
        }
        //无环返回nullptr
        return nullptr;
    }
};

总结

两个方法各有利弊，方法一不需要数学推导，思路简单，但是空间复杂度较高，方法二需要数学推导，但是只需要在判断入环节点位置时