🐉 127.单词接龙
字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk:
- 每一对相邻的单词只差一个字母。
- 对于
1 <= i <= k 时,每个 si 都在 wordList 中。注意, beginWord 不需要在 wordList 中。 sk == endWord
给你两个单词 beginWord 和 endWord 和一个字典 wordList ,返回 从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列,返回 0 。
思路
基本思想
为了从beginWord变换到endWord,需要将每一步的变换都记住,从而从中找到一个最短的变换路径,也就是求图中两个顶点的最短路径问题,如下图所示:
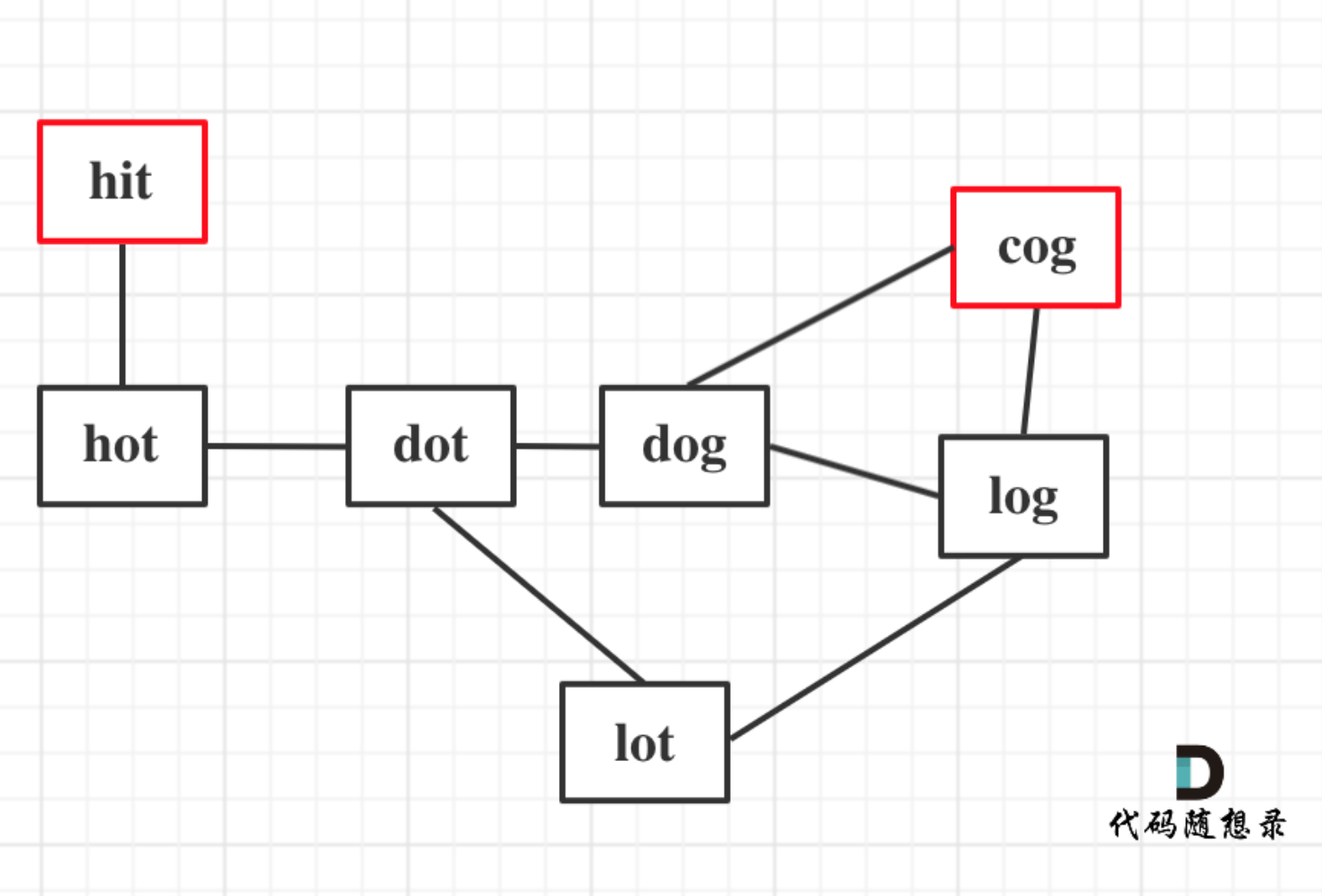
从开始变换到结束有很多条路径,还需要找到最短的路径,所以分成两个任务:
- 找到所有的路径
- 从所有的路径中找到最短的
下面是具体的分析思路:
相当于从一个单词到下一个单词, 只能变换一个字母,所以对于一个单词来说,针对单词的每个位置,都可以有26种变换方法,所以对于一个单词来说,一共有word.size()*26种变换方法,所以我们拿到一个单词,需要执行这么多次变化,来看其中的某一种是不是出现在文中所给的字典中,如果出现在所给的字典中,那么说明当前变换有效
当前单词的所有有效变换找到之后,需要将这些有效变换进一步的进行变换,直到其中的某一步找到endWord,或者说所有的变换都找完了。还是没找到endWord,此时说明无法变换到endWord,直接返回0
整体来说,需要从beginWord出发,寻找下一阶段的所有能变换的单词(只差一步的单词),再从下一阶段的所有单词出发,找到更下一阶段的单词,从当前阶段到下一阶段,需要让步数+1,每到达一个新的单词,相当于做了一次变换
我们需要三个容器,一个容器记录当前字典中的单词,使用unordered_set,查询更快,一个容器记录变换路径上的所有单词以及到变换到这个路径需要多少步,所以使用unordered_map,另外一个就是记录当前所有变换的单词,以便下一步取出这些单词中的一个进行进一步的变换
更简单的办法就是利用图的广度优先遍历,每一层存储的都是同一步能到达的所有顶点,下一层就是当前层的所有顶点走一步能够到达的所有顶点,一旦某个顶点是终点,就找到了结果
执行流程
将所给的vector字典转换成unordered_set字典
判断字典中是不是存在endWord,如果不存在的话,直接返回0
将beginWord加入队列和map中,代表从这个单词出发开始遍历
只要队列不为空,就一直变换
针对队列中的每一个单词,都需要进行遍历,依次变换每个位置上的字母,看是不是变换成了字典中的单词
一旦变换成了字典中的单词,无非是两种情况:
- 变换成了endWord,此时直接返回变换到当前单词的路径数+1
- 变换成了字典中的单词,但是不是重点
- 如果当前单词没有被访问过,那么将当前单词分别加入map和队列中
- 如果当前单词访问过了,为了避免死循环,直接跳过当前单词
当队列为空都没有找到endWord,说明无法变化到endWord中,此时返回0
代码
根据以上分析,得出以下代码 :
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
public:
int ladderLength(string beginWord, string endWord, vector<string>& wordList) {
// 将vector转成unordered_set,提高查询速度
unordered_set<string> wordSet(wordList.begin(), wordList.end());
// 如果endWord没有在wordSet出现,直接返回0
if (wordSet.find(endWord) == wordSet.end()) return 0;
// 记录word是否访问过
// <word, 查询到这个word路径长度>
unordered_map<string, int> visitMap;
// 初始化队列
queue<string> que;
que.push(beginWord);
// 初始化visitMap
visitMap.insert(pair<string, int>(beginWord, 1));
//队列不为空就一直访问
while(!que.empty()) {
string word = que.front();
que.pop();
// 这个word的路径长度
int path = visitMap[word];
//对单词的每一个位置都替换26次
for (int i = 0; i < word.size(); i++) {
// 用一个新单词替换word,因为每次置换一个字母
string newWord = word;
for (int j = 0 ; j < 26; j++) {
newWord[i] = j + 'a';
// 找到了end,返回path+1
if (newWord == endWord) return path + 1;
// wordSet出现了newWord,并且newWord没有被访问过
if (wordSet.find(newWord) != wordSet.end()
&& visitMap.find(newWord) == visitMap.end()) {
// 添加访问信息
visitMap.insert(make_pair(newWord, path + 1));
que.push(newWord);
}
}
}
}
return 0;
}
};
|
java代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
//与上一个基因变化序列的方法类似
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
//单词序列中
if(!wordList.contains(endWord))
return 0;
Queue<String> queue=new LinkedList<>();
int res=1;
int[] visited=new int[wordList.size()];
queue.offer(beginWord);
while(queue.size()>0){
++res;
//遍历当前层的所有节点
int size=queue.size();
for(int i=0;i<size;++i){
String temp=queue.poll();
//针对当前层的当前节点,从字典中取出只差一位的所有未遍历节点
for(int j=0;j<wordList.size();++j){
String word=wordList.get(j);
if(visited[j]==0){
int diff=0;
//看字典中的当前单词与当前层中的当前单词相差几个位置
for(int k=0;k<word.length();++k){
if(temp.charAt(k)!=word.charAt(k))
++diff;
}
//两个单词只差一步
if(diff==1){
if(word.equals(endWord))
return res;
visited[j]=1;
queue.offer(word);
}
}
}
}
}
return 0;
}
}
|
总结
就是将当前单词的每一个位置都变换26次,如果形成了字典中的单词,那么就记录当前单词,形成一个新的单词,此时变换的路径数就要+1,我们使用一个unordered_map来记录这个对应关系。
使用广度搜索,一旦在变换的途中遇到了endWord,那么就返回对应的路径数,因为广度搜索遇到了endWord一定是最短的路径
更加简洁的通用办法就是将问题转换成图的广度优先遍历问题,第i层的节点代表从起点出发走i步能够到达的节点,然后针对当前层的所有节点,从字典中查询到只差一个元素的节点作为下一层的节点,就这样进行广度优先遍历,每到一层就将结果数+1,一旦找到了结果节点就直接返回当前层的层数即可
