122.买卖股票的最佳时机II

发表于： 分类于：
字数： 1405 阅读：≈ 3分钟

💰122.买卖股票的最佳时机II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候最多只能持有 一股 股票。你也可以先购买，然后在同一天出售。

多次买卖，且买卖时间不能重合，但是卖和买可以在同一天，所以需要将多次买卖的利润求和

返回 你能获得的最大利润 。

示例

示例 1:

  • 输入: [7,1,5,3,6,4]
  • 输出: 7
  • 解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。

示例 2:

  • 输入: [1,2,3,4,5]
  • 输出: 4
  • 解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3:

  • 输入: [7,6,4,3,1]
  • 输出: 0
  • 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

提示：

  • 1 <= prices.length <= 3 * 10 ^ 4
  • 0 <= prices[i] <= 10 ^ 4

思路

贪心思路

如果只能买卖一次，那么就直接更低点买入，更高点卖出，有更大利润就更新，但是这里是可以买卖多次，也就是说卖出去之后还可以买卖，但是必须卖出去之后才能买入，也就是说卖卖的时间段不能交叉

这里借鉴一次卖出的思想，将当前的每一天都当作最高点进行卖出，然后在前一天进行买入，统计两天之间的利润，这样一段时间的利润就被分成了每两天之间的利润和

之后统计两天之间大于0的利润之和，也就是统计所有盈利的部分，去除亏损的部分，由于是两天之间的利润，为最小单位，所以不会出现重叠，符合题目要求

形成的利润数组如图所示：

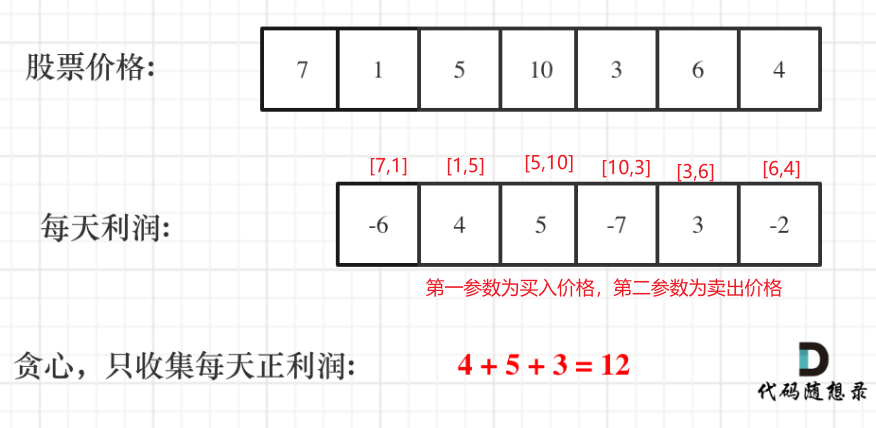
image-20230531191911142

不是一次买入的更低就买，更高就卖，而是两天一买卖，最后统计所有盈利的部分，防止出现重叠，且可以使得利润最大化

DP思路

由于买入时手上不是一分钱都没有，而是有之前买卖股票盈利的钱，所以当前的花销dp[i][0]应该是之前的盈利减去当前股票的价格，由此得到的递推方程为： $$ dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i])\ dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]) $$ dp[i][0]代表第i天买入之后手上还剩多少钱

dp[i][1]代表第i天卖出之后手上还剩多少钱

贪心执行流程

定义一个sum存放最终的利润和，其初值为0，遍历容器，每两天买卖一次，由于上一次卖和这一次买可以在同一天，所以可以使用prices[i+1]-prices[i]来计算利润

计算完利润之后，大于零的利润会被统计到sum中，运行结束返回sum即可

DP执行流程

  1. 初始化dp数组，注意dp[0][0]=-prices[0]
  2. 按照递推方程统计结果
  3. 返回最后手上剩多少钱作为最终的结果

代码

根据以上分析，得出以下代码：

贪心 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //存放最终利润
        int sum=0;
        for(int i=0;i<prices.size()-1;++i){
            //两天之间利润大于零就统计
            if((prices[i+1]-prices[i])>0){
                sum+=prices[i+1]-prices[i];
            }
        }
        return sum;
    }
};

DP 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        if(prices.size()==1)
            return 0;
            vector<vector<int>> dp(prices.size(),vector<int>(2,0));
            //初始化数组
            dp[0][0]=-prices[0];
            for(int i=1;i<prices.size();++i){
                //低就买入
                dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);
                //高就卖出
                dp[i][1]=max(dp[i-1][1],prices[i]+dp[i-1][0]);
            }
            return dp[prices.size()-1][1];
    }
};

总结

题目中共有两个问题需要解决：

  1. 多次买入和卖出的时间点不能交叉

    直接将买卖的时间段拆分成最小单元，这样就不会交叉

  2. 统计最大利润

    由于是两天一买卖，所以只要是盈利的部分都可以进行统计

上述两个问题解决完之后，就可以统计出最大的利润，其中的关键点就是将买卖的时间段进行切分，这样就不会交叉，之后直接贪心的将所有盈利的部分统计起来即可

DP的核心思想就是关注任意时刻手上还剩多少钱

二者关心的点不一样