1143.最长公共子序列

发表于： 分类于：
字数： 885 阅读：≈ 2分钟

😄1143.最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。 两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

思路

基本思想

与 718题 很像，但是本题是求公共的子序列长度，子序列不要求连续，只要相对位置不改变就可以成为子序列，所以在比较时不是不相等就不比较，当当前两个元素不相等，可能之前的元素有相等的，所以还需要看之前的元素是不是相等

本题中的dp[i][j]代表以第i个元素和第j个元素结尾的两个字符串的最长公共子序列长度

具体这个看之前的元素是不是相等的判断逻辑 体现在代码中为：

1
2
3
4
5

if (text1[i - 1] == text2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

只要当前的两个元素不相等，那么就返回之前的元素中子序列长度最长的结果

体现在图中就是：

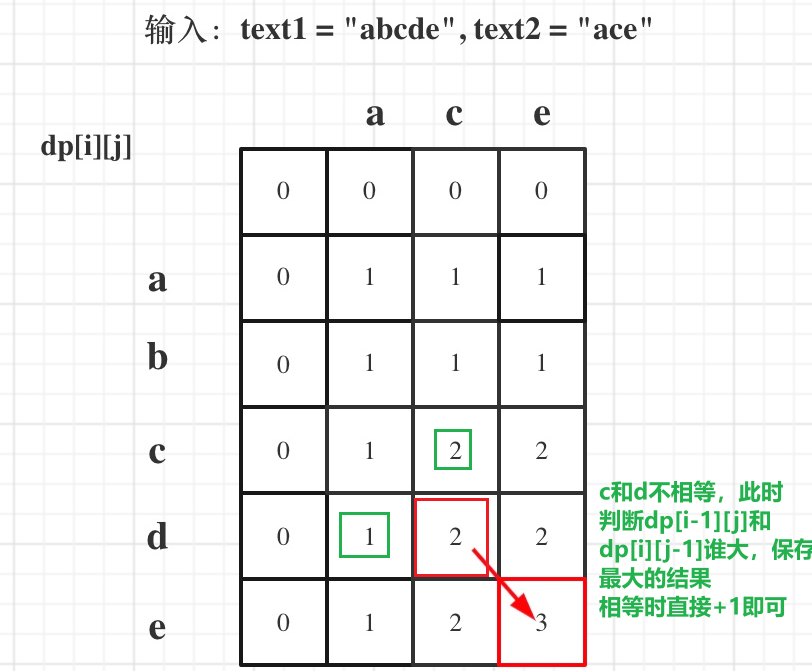
image-20230630192118939

当前的元素不相等时，说明以当前两个元素结尾的字符串公共子序列长度不可能增加，就选择最长的公共子序列长度作为当前的结果，更新当前的结果供后面的元素匹配时使用

主要理解这个图的更新过程，求的是当前位置的最长公共子序列

执行流程

  1. 初始化dp数组，让其都为0
  2. 根据递推公式更新dp数组
  3. 返回最终的元素当成最后的结果

代码

根据以上分析，得出以下代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size()+1,
                                vector<int>(text2.size()+1,0));
        for(int i=0;i<text1.size();++i){
            for(int j=0;j<text2.size();++j){
                if(text1[i]==text2[j]){//匹配说明最长公共子序列长度要增加
                    dp[i+1][j+1]=dp[i][j]+1;
                }else{//不匹配就统计以这两个元素结尾的最长公共子序列
                    dp[i+1][j+1]=max(dp[i][j+1],dp[i+1][j]);
                }
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

总结

主要分为两点：

  1. 当前两个元素匹配时，最长公共子序列的长度肯定最长

  2. 当前两个元素不匹配时，说明有一个元素多余了，此时就看是谁多余了

    使用max函数统计当前两个元素去掉其中一个的最长公共子序列长度作为当前的结果

    以便以后面的元素使用

统计以当前两个元素结尾的字符串的最长公共子序列长度即可

  • 看懂图片中的更新过程