解决背包问题的思路

发表于： 分类于：
字数： 3890 阅读：≈ 8分钟

🎒解决0-1背包问题的思路

分析最基本的0-1背包的动态规划解题思路，基本步骤从最开始的初始化价值数组，确定递推方程到最后的更新价值数组得到最终答案

之后再引出完全背包的问题，唯一的区别就是物品可以装入任意次

总结来看除了排列问题需要先遍历背包容量，其余都先遍历物品，然后完全背包由于物品可以重复放入，所以可以从小到大，小的更新了，大的也能用到

核心就是确定递推公式和初始化方案

引言

0-1背包就是当前背包总容量为n，有一堆物品，每个物品的重量为weight[i]，每个物品的价值为value[i]，最终目的是为了让背包中的物品尽可能的价值大，某些性价比不高的物品可以丢弃不装入背包，选择性的装一些价值尽可能大，重量尽可能小的物品

当前背包容量下形成的最大价值与小容量下形成的最大价值有关

存放最终的背包价值的dp数组有两种，二维和一维，先分析二维再将二维降成一维

完全背包与01背包唯一的区别就是物品可以装入任意次

前期准备

  1. 物品

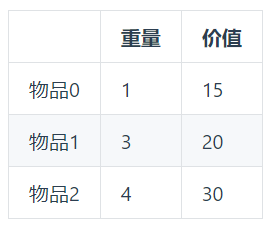
    image-20230619193812919

  2. 二维dp数组初始化

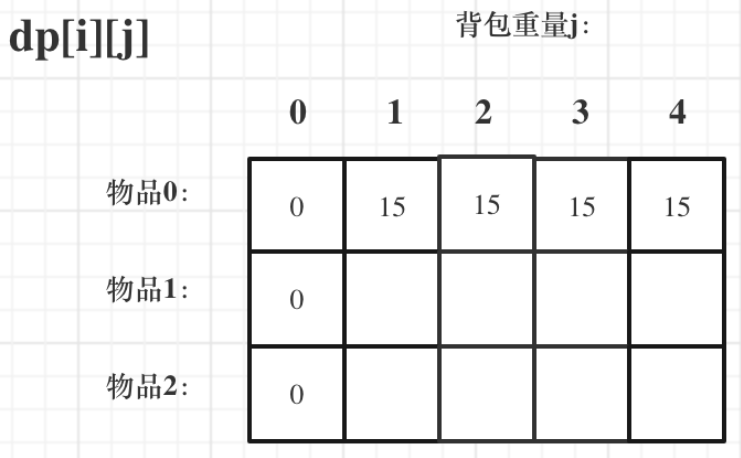
image-20230619193844382

  1. 一维dp数组初始化

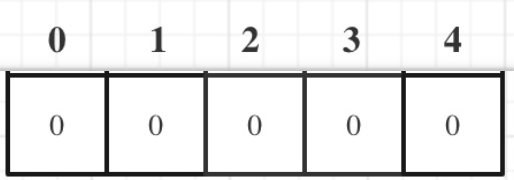
    image-20230619202517970

0-1背包

直接提供代码来进行分析

整个代码是针对每个物品，对于不同的背包容量来统计最后的价值，当所有物品都尝试过之后，返回最终的结果（dp数组最后的值）

二维dp 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

void test_2_wei_bag_problem1()
{
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagweight = 4;
    // 二维数组
    //dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
    // 初始化，一旦能放下物品0，就先只放物品0
    for (int j = weight[0]; j <= bagweight; j++)
    {
        dp[0][j] = value[0];
    }
    // weight数组的大小 就是物品个数
    for (int i = 1; i < weight.size(); i++)
    { // 遍历物品
        for (int j = 1; j <= bagweight; j++)
        { // 遍历背包容量，从1开始才有意义
            if (j < weight[i])//当前背包放不下当前物品
                dp[i][j] = dp[i - 1][j];
            else{//当前背包放得下当前物品，主要看放下之后价值是否增加
                int weight_not=dp[i - 1][j];
                int weight_put=dp[i - 1][j - weight[i]] + value[i];
                dp[i][j] = max(weight_not, weight_put);
            }
        }
    }
    cout << dp[weight.size() - 1][bagweight] << endl;//返回右下角的结果
}

执行流程

递推公式为： $$ dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]) $$

  1. 对dp数组进行初始化，其中dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

  2. 对每一个物品，看不同的背包容量形成的价值是多少，装入物品时分为两种情况：

    • 当前背包容量放不下当前物品，那么当前位置的dp就是不放当前物品的价值，也就是：

      dp[i][j] = dp[i - 1][j]

    • 当前背包容量放得下当前物品，此时又分为两种情况：

      • 剩余容量可以直接装下当前物品i,直接放，价值肯定增加，比如容量为4时放物品1，即使背包中有了物品0也可以再放一个物品1
      • 剩余容量无法直接装下当前物品i，例如容量为3时放物品1，此时背包中已经有了物品0，需要将物品0取出来

    • 两种情况都将放入当前物品的价值与不放当前物品的价值进行比较，取最大值

      1
2
3

      int weight_not=dp[i - 1][j];//不放当前物品
int weight_put=dp[i - 1][j - weight[i]] + value[i];//放当前物品
dp[i][j] = max(weight_not, weight_put);

  3. 最大值取不放当前物品的价值说明当前背包容量无法直接容纳当前物品，取出之前的物品放入当前物品之后的价值还不如不放，因为价值没有变大

  4. 最大值取放当前物品的价值有两种情况：

    • 当前背包可以直接装下当前物品，不用取出任何物品，肯定价值会变大

    • 当前背包无法直接装下当前物品，但是取出一些物品之后装入当前物品，价值也变大

      这两种情况包含在j-weight[i]中

一维dp 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

void test_1_wei_bag_problem()
{
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;
    //dp[j]表示：容量为j的背包，所背的物品价值可以最大为dp[j]。
    vector<int> dp(bagWeight + 1, 0);
    for (int i = 0; i < weight.size(); i++)
    { // 遍历物品
        //一旦背包初始容量小于当前物品重量，一定装不下，当前物品直接舍弃
        //也就是到j<weight[i]的时候，当前物品就不用装进背包了，也装不进去
        //即拿出来判断的物品一定是可以装下的
        //这里的背包容量从大到小，防止物品的重复放入
        for (int j = bagWeight; j >= weight[i]; j--)
        { // 遍历背包容量，背包容量从大到小
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;//返回最大容量的结果
}

执行流程

递推公式为： $$ dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) $$

  1. 初始化dp数组全为0，代表不管背包容量多大都不放物品

  2. 从后向前递减背包容量，不从前向后的原因是为了防止物品被多次放入，因为放入当前物品时如果可以直接放入，那么背包之前的价值会被累加，也就是： $$ dp[1] = dp[1 - weight[0]] + value[0] = 15 $$ $$ dp[2] = dp[2 - weight[0]] + value[0] = 30 $$

    背包容量为2时物品1可以直接放入，从前向后遍历的话剩下的空间还会放入一次物品1，而从后向前遍历的话即使剩余空间可以放入物品1，由于dp初始化为0，还没来得及更新为15，所以不放入,体现在公式中为： $$ dp[2] = dp[2 - weight[0]] + value[0] = 15 $$ $$ dp[1] = dp[1 - weight[0]] + value[0] = 15 $$

    由于dp[2 - weight[0]]初始化为0，代表物品1不被装入

    不理解的话可以正向和反向debug一遍

  3. 对每一个物品，都判断产生的价值，存放物品有两种情况：

    • 当前物品可以直接放下，背包价值直接递增

    • 当前物品不能直接放下，背包中的部分物品需要取出，然后在判断取出之后装入当前物品的价值谁大

    • 形成的代码判断逻辑为：

      1
2
3

      int weight_not = dp[capacity];
int weight_put = dp[capacity - weight[stuff]] + value[stuff];
dp[capacity] = max(weight_not, weight_put);

  4. 相比与二维dp来说，只要背包的初始容量小于当前物品的容量，就直接舍弃当前物品，因为无论如何当前物品都装不下

完全背包

代码 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

void test_CompletePack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;
    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        //背包容量从小到大，因为完全背包中物品可以重复放入
        for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    cout << dp[bagWeight] << endl;
}

执行流程

在0-1背包中的一维dp中，背包的容量是从大到小，先更新大的再更新小的，目的是为了防止物品重复被放入

这个重复被放入在推导的过程中体现在： $$ dp[1] = dp[1 - weight[0]] + value[0] = 15 \dp[2] = dp[2 - weight[0]] + value[0] = 30 $$ 容量从小到大遍历的话，小的更新之后，大的会用到小的形成的结果，在公式中体现为物品1被放入多次

0-1背包需要避免这种情况

完全背包就需要这种情况，所以完全背包的背包容量从小到大

至于背包和物品谁先遍历，0-1背包的一维版本需要在外层遍历物品，内层遍历容量

完全背包先遍历谁都可以，只要保证物品可以重复加入即可

重复加入就是大容量的价值依赖于小容量的价值，如果从前到后遍历，那么小容量就会先更新，累积到大容量之后大容量还可以放下物品时，物品就会被重复放入

如果从后向前遍历，即使大容量放了物品，由于从后向前小容量还没有更新，并且小容量的价值只依赖于更小容量的价值，所以物品不会被重复放入

可以说0/1背包与完全背包的区别就是在内层背包容量的变化上

0/1背包是从大到小，完全背包是从小到大

分类

0-1背包

0-1背包的一维dp伪代码为：

1
2
3
4
5

for(int i=0;i<nums.size();++i){//遍历物品
	for(int j=capacity;j>=nums[i];--j){//遍历背包容量，从大到小
		dp[j]=max(dp[j],dp[j-nums[i]]+value[i]);
	}
}

背包的容量从大到小遍历，防止==元素的重复放入==

完全背包

完全背包的伪代码为：

1
2
3
4
5

for(int i=0;i<nums.size();++i){//遍历物品
	for(int j=nums[i];j<=capacity;++j){//遍历背包容量，从小到大
		dp[j]=max(dp[j],dp[j-nums[i]]+value[i]);
	}
}

背包容量从小到大遍历，使得元素可以重复放入

组合

当不考虑物品的放入顺序时，也就是先放入物品1再放入物品3和先放入物品3再放入物品1没有区别时，伪代码为：

1
2
3
4
5

for(int i=0;i<nums.size();++i){//遍历物品
	for(int j=nums[i];j<=capacity;++j){//遍历背包容量
		dp[j]+=dp[j-nums[i]];//这里的加以nums[i]结尾，剩下的元素有多少种可能
	}
}

不考虑放入顺序时，先遍历物品，此时一定是先放入编号小的物品

排列

考虑放入物品顺序时，也就是物品1，物品3的放入顺序和物品3，物品1的放入顺序形成的结果不一样时，伪代码为:

1
2
3
4
5
6
7

for(int j=0;j<=capacity;++j){//遍历背包容量
	for(int i=0;i<nums.size();++i){//遍历物品
        if(j-nums[i]>=0){//当前物品可以放下才统计
            dp[j]+=dp[j-nums[i]];
        }
	}
}

为了使[1,3]和[3,1]不一样，先遍历背包容量，==这样保证会出现[3,1]的情况==，为什么可以保证

组合就是正常的背包问题，排列需要先遍历背包容量，其余都是先遍历物品

总结

0-1背包问题主要是判断当前物品能不能放进当前背包，放进去之后能不能增加背包的整体价值

对于二维dp来说，当前物品的判断逻辑很复杂

如果无法理解就直接debug上面的代码，重点注意背包容量为3时放物品1，背包容量为4时放物品1，背包容量为3时放物品2

  1. 背包容量为3时放物品1是将背包中原有的物品0取出来放入物品1，因为虽然无法直接装下物品1，但是取出一些物品之后装入当前物品，价值变大为20

  2. 背包容量为4时放物品1是可以直接将物品1放入，此时背包中有物品0和物品1，价值肯定增大

  3. 背包容量为3时放物品2是怎样都无法放入，直接不放，递推公式dp[i][j] = dp[i - 1][j]

对于一维dp来说，当前物品只有如何放不放的问题，因为拿出来判断的物品一定是可以放下的（容量的起点就是物品的大小），我们只需要关心当前物品放入之后价值是否会增加

所以最终的递推公式为： $$ dp[j] = max(dp[j], dp[j - weight[i]] + value[i]) $$ 核心就是确定递推公式以及初始化方案，一维dp中背包容量从大到小是为了防止物品重复装入，并且不放当前元素的价值为dp[j]，而不是dp[j-1]

完全背包唯一的区别就是改变了背包容量的遍历方向，变成了从小到大

总结成一句话就是，除了排列，都是先遍历物品，再遍历背包容量，完全背包的元素可以重复放入，背包容量可以从小到大