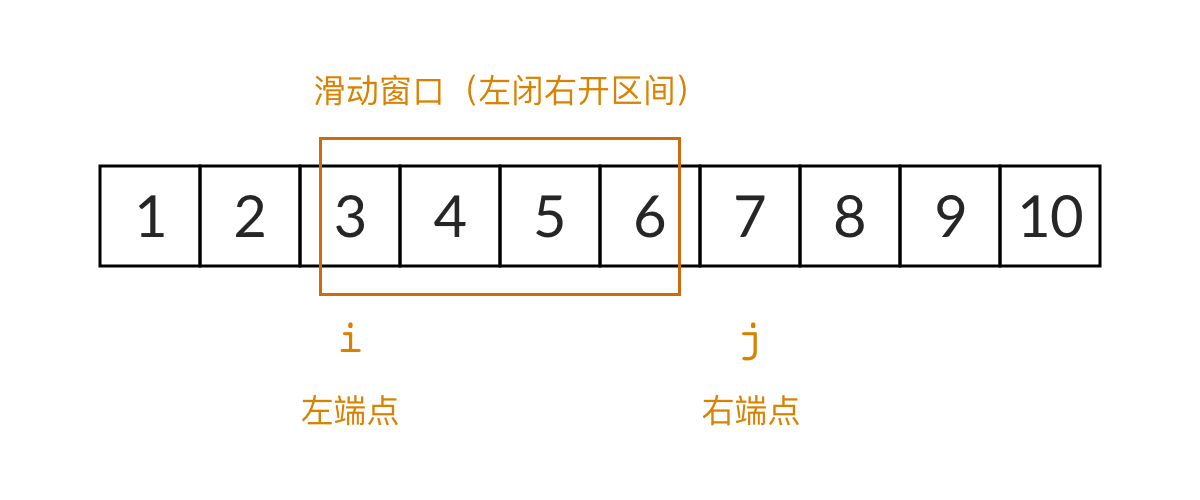
🚍 滑动窗口
根据灵神的滑动窗口
题单
总结的滑动窗口模版,主要分为两个大类,重点在于变长滑动窗口时如何减小时间复杂度
定长滑动窗口
定长滑动窗口的精髓是固定k
所谓的定长,指的是窗口的长度不变,题目中一般会给出长度为K的限制,此时只需要一个单指针right就可以固定住窗口大小,窗口滑动时,左边窗口的位置可以用right-k来计算,不符合要求的元素扔掉即可,模版为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
//一般题目会给定数组或者字符串,以及窗口的固定大小
public void staticWindow(int[] arr, int k) {
int right=0;
while(right<arr.length){
//在这里累加或者统计窗口中符合条件元素的个数
if(arr[right++] 满足条件)
//统计
//形成了k大小的窗口
if(right>=k){
//针对当前窗口做业务
//窗口滑动,删除左边的元素
sum-=arr[right-k];
}
}
//返回结果
}
}
|
变长滑动窗口
求最大最小
求最大和最小在不同的地方更新,最小在内部,最大在外部
变长滑动窗口的精髓是找到边界条件
变长滑动窗口只有两个操作,并且需要两个指针,因为此时窗口大小是变化的:
- 变长,只要没触发边界条件就一直变长
- 缩短:一旦触发边界条件,就开始缩短
根据这种分析,得到一个滑动窗口的模版:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int dynamicWidow(int[] nums) {
//变长窗口必须两个指针
int right = 0, left = 0;
while (right < nums.length) {
//不断滑动,有可能是累加窗口中的元素值,也有可能是统计元素出现次数
while(left<=right&&false){//这里的left<=right看情况添加
//求最小值在这里尝试更新结果
++left;
}
//求最大值在这里尝试更新结果
//滑动
++right;
}
// 最后一个窗口别漏掉
res = Math.max(res, right - left);
return res;
}
}
|
最子数组个数
当求的是满足条件的子数组的个数时,此时依次从每个元素出发,然后向后统计,只有有一个数组符合要求,后面的一定符合要求:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int countArray(String s) {
int res = 0;
char[] ch = s.toCharArray();
for (int i = 0; i < ch.length; ++i) {
//重置辅助变量
//分别从每个i向后出发
for (int j = i; j < ch.length; ++j) {
// 统计
if (true) {// 满足条件后面的就不需要统计了
res变大;
break;
}
}
}
//返回结果
return res;
}
}
|
这种方式很直观,但是容易超时,因为内部套了一层循环,并且有很多重复步骤,所以需要简化:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public int countArray(int[] nums) {
int left = 0, right = 0, res = 0, num = 0;
while (right < nums.length) {
//右边界不断滑动
while (true) {//刚好满足条件
//缩小左边界
left++;
}
// 到这里说明左边界减小一步刚好有一个符合要求的子数组
res += left;//只有移动了才会加,因为left的初值为0
//或者这里刚好有一个符合要求的子数组
res=right-left;
}
return res;
}
}
|
上面两种方法需要斟酌,如果子数组满足条件是超过某一个条件,两个模版都可以使用,如果子数组满足条件是不超过某一个条件,此时建议使用第一个模版
第二个模版如何作用到条件是小于等于的题目上的:一旦大于就缩小左边界,找到一个[left,right]满足条件后,所有的left<right都符合条件,相当于小于等于向右计算,大于等于向前计算
多指针
这种题目一般找到一个窗口后,前面或者后面只有一部分满足条件,不能直接像最小数组个数一样累加,而是需要使用多指针过滤满足条件的元素
比如说统计1出现的次数,数组中只有0和1,当前窗口中的元素为[1,0,0,1],只要左边的1前面还是0,就符合条件,所以我们可以使用多指针来找到左边1前面0的个数
其实也可以用最小数组个数的第一个模版来做题,但是这个模版容易超时
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public int numberOfSubarrays(int[] nums, int k) {
int numSlow = 0, numFast = 0;
int leftSlow = 0, leftFast = 0;
int right = 0, res = 0;
while (right < nums.length) {
++numFast;
++numSlow;
// 减小到刚好小于
while (leftFast <= right && numFast >= k) {
--numFast;
}
// 减小到刚好等于
while (leftSlow <= right && numSlow > k) {
--numSlow;
}
// 小于到等于之间的数都可以成为答案
res += leftFast - leftSlow;
++right;
}
return res;
}
}
|
