平衡二叉树和红黑树
😄平衡二叉树和红黑树
介绍平衡二叉树的插入和删除操作,红黑树的基础理论以及红黑树的插入和删除
平衡二叉树
插入
- 首先在树上进行搜索,找到要插入的位置,插入之后若出现不平衡则调整
- 插入的节点肯定是在叶子节点上,从当前插入节点自底向上找到第一棵不平衡子树的根节点root
- 当前节点到根节点有一条路径,从这条路径自顶向下找到从root开始的三个节点
- 三个节点形成一个平衡二叉树x,然后将不平衡子树的剩余节点直接插入x中即可,插入时需要保留原来的父子和兄弟关系
以上方法是通法,不再需要考虑
LL,LR,RR,RL分类的情况
举例:
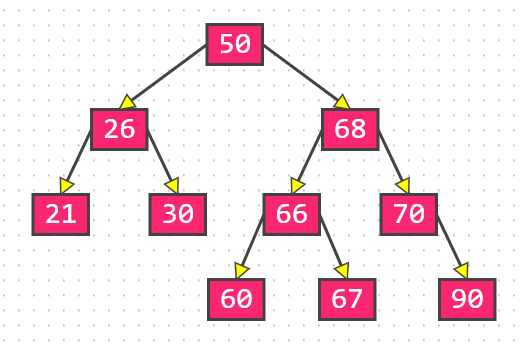
插入63,出现不平衡情况:
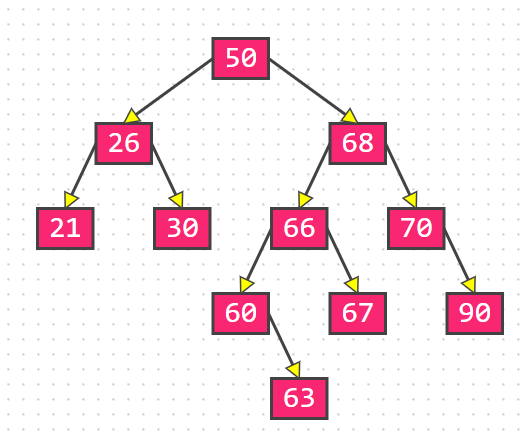
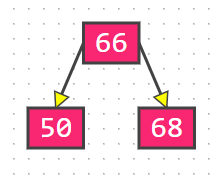
从63向上找到第一个不平衡子树的根节点为50,50到63的路径为:[50,68,66,60,63],前三个节点为[50,68,66],组成一个二叉树:
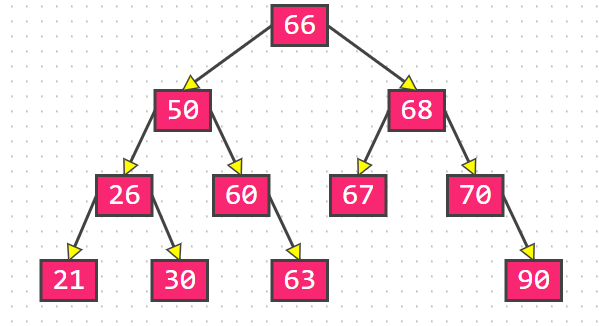
之后将剩下的[21,26,30,60,63,67,70,90]直接插入即可,插入时原来的父子和兄弟关系需要保留:
删除
- 按照二叉搜索树的方式进行删除,最复杂的情况就是待删除节点左右子树都不为空,此时将此节点的左子树接入右子树的最左边节点, 参考
- 判断整棵树是否平衡,不平衡的话借鉴插入的思想,自底向上找到最小的不平衡二叉树进行调整,调整的思路与插入时一样
- 将最小不平衡子树的最底层叶子节点当作终点找到一条路径,然后调整,如果最底层叶子节点有多个,那么就任选一个,但是推荐选靠右的27
举例,删除2:
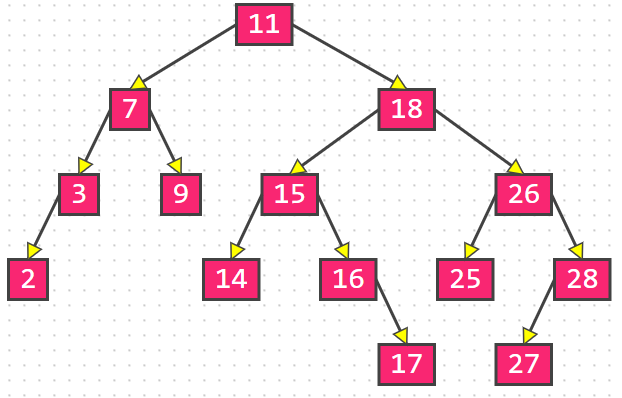
删除之后不平衡,最小不平衡子树的根节点为11,最底层叶子节点为17和27,任选一条路径调整即可,这里推荐选择靠右的27:
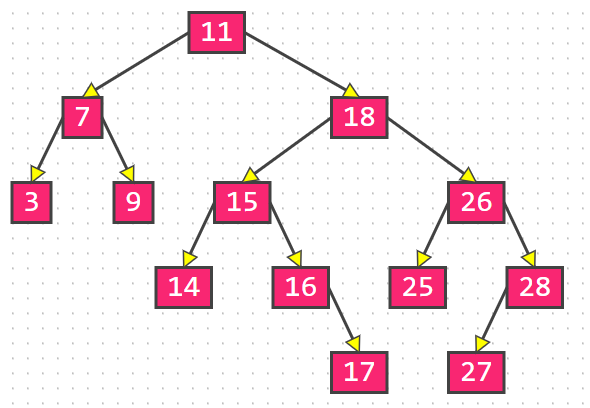
调整之后为:
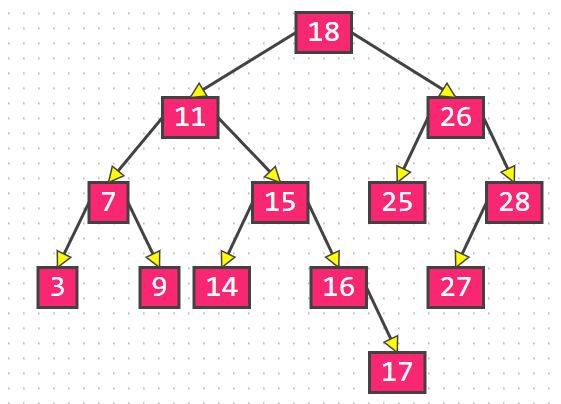
AVL总结
平衡二叉树的调整时插入和删除的基础,插入和删除参考二叉搜索树的插入和删除,之后就是将插入和删除之后的树调整成平衡二叉树,主要步骤如下:
- 自底向上找到最小的不平衡二叉树的根节点root
- 从root出发找一条到最底层节点的路径,取出前三个节点形成平衡二叉树x
- 剩下的节点在不改变父子和兄弟关系的前提下插入x即可
- 插入只用调整一次,删除可能需要调整多次
二叉排序树的插入和删除+平衡二叉树的调整
红黑树
为了提高系统的查询效率,引入红黑树,那么为什么不使用平衡二叉树呢,因为平衡二叉树的调整太消耗时间,一旦节点变化,那么就要调整,导致平衡二叉树花费了大量的时间进行调整,所以出现频繁的插入和删除时,平衡二叉树性能并不是很好
基于以上分析引入了红黑树,他继承了平衡二叉树的平衡特性和搜索特性,不会出现二叉搜索树的极端情况,同时又放宽平衡的条件,使得面对大量的插入和删除的情况时性能也变得很好
性质
- 节点有红黑两种颜色
- 根节点一定是黑色的
- 叶子节点(不存储元素)一定是黑色的
- 红色节点的两个孩子节点都是黑色的,黑色节点的孩子可红可黑
- 从一个节点出发,到任意一个叶子节点的路径上都包含相同数量的黑色节点
基于以上原则,会将待插入节点设置为红色在进行插入
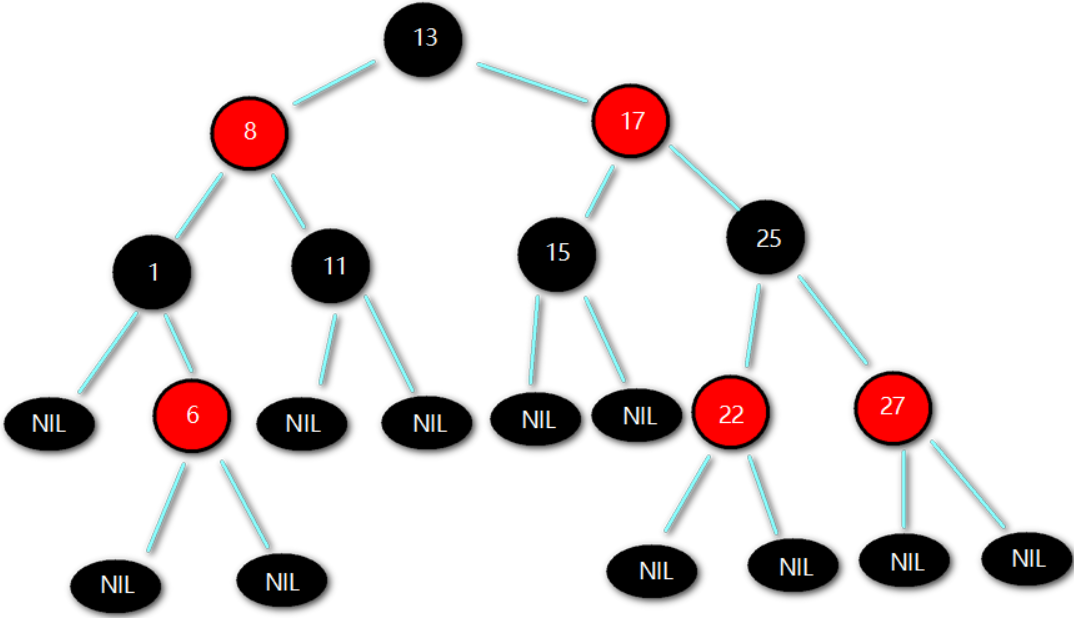
最后一个属性类似于平衡二叉树中的平衡因子,保证红黑树的平衡性
一旦出现上述五个性质中的一个不满足,就视为不平衡,需要进行调整,一共有三种调整方式:变色、左旋、右旋,旋转类似于平衡二叉树的旋转
插入
红黑树插入时默认待插入节点是红色的,并且插入节点时与二叉搜索树一样要先搜索插入位置,然后插入之后将其调整,一共分为以下几种情况:
空树
此时可以直接插入,待插入节点变成根节点,但是由于根节点只能是黑色,待插入节点默认是红色,所以需要变色:

存在相同节点
分为两种情况
- 节点颜色为黑色,待插入节点默认为红色,所以需要先变色 ,再更新
- 节点颜色为红色,待插入节点默认为红色,直接更新
插入100,属于第一种情况,直接更新节点的信息即可:
插入父节点为黑色
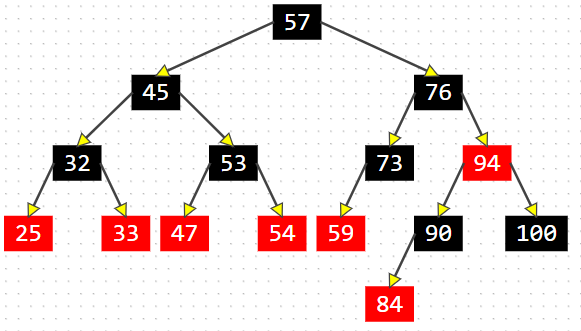
由于待插入节点默认为红色,并且父节点为黑色,所以红黑树的五个性质一定满足, 直接插入即可,插入之后一定符合平衡条件
插入101:
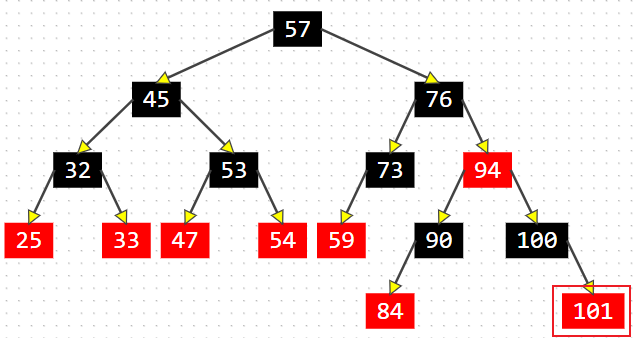
插入父节点为红色
简单分析以下,如果插入的父节点为红色节点,那么父节点不可能时根节点(性质1)
同时父节点的父节点一定不是红色节点(性质4),也就是说父节点一定在红黑树的中间位置,
此时有两种情况:
父节点和叔叔节点都为红色(爷爷节点是黑色),对应在上图,父节点就是47
父节点为红色,叔叔节点为空(黑色),对应在上图,父节点就是84
- 插入之后形成LL或者RR
- 插入之后形成LR或者RL
对于情况1,进行如下处理:
- 父亲和叔叔变黑
- 爷爷变红
- 矛盾向上转移,可以出现红黑相连和黑黑相连,不能出现红红相连
总结:可以出现连续的黑色,不能出现连续的红色,并且连续的红色尽量让其出现在上层,
向树中插入7:
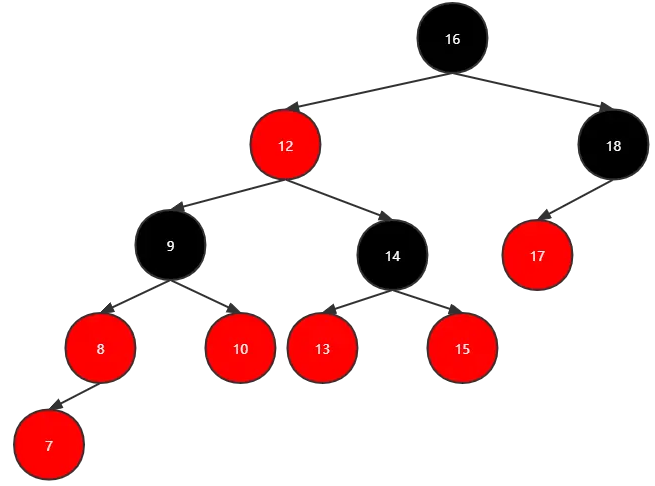
父亲和叔叔节点变黑,爷爷节点变红:
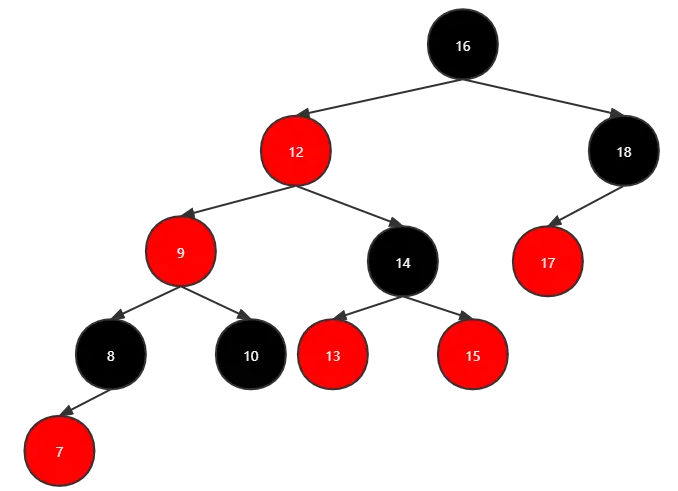
爷爷节点9红色,所以爷爷节点9的父亲节点12需要变成黑色,12 的父亲节点16需要变成红色:
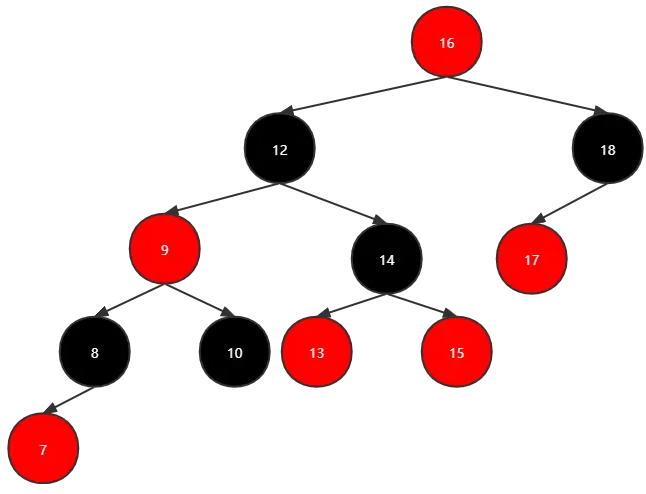
此时再进行旋转,从较高的一边选取三个节点形成红黑树,之后剩下的节点插入这个红黑树即可,参考平衡二叉树的调整:
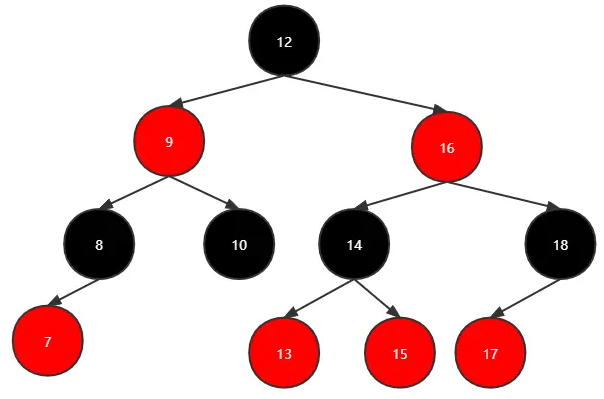
对于情况2,需要进行以下处理:
取决于待插入节点的大小,可插入到父亲节点的左孩子或者右孩子,于是又出现两种情况:
1.插入之后形成LL或者RR
- 直接将父亲节点变成黑色
- 爷爷节点变成红色
- 进行旋转,以父亲节点的黑色为根节点形成小红黑树插入到大红黑树
向树中插入13:
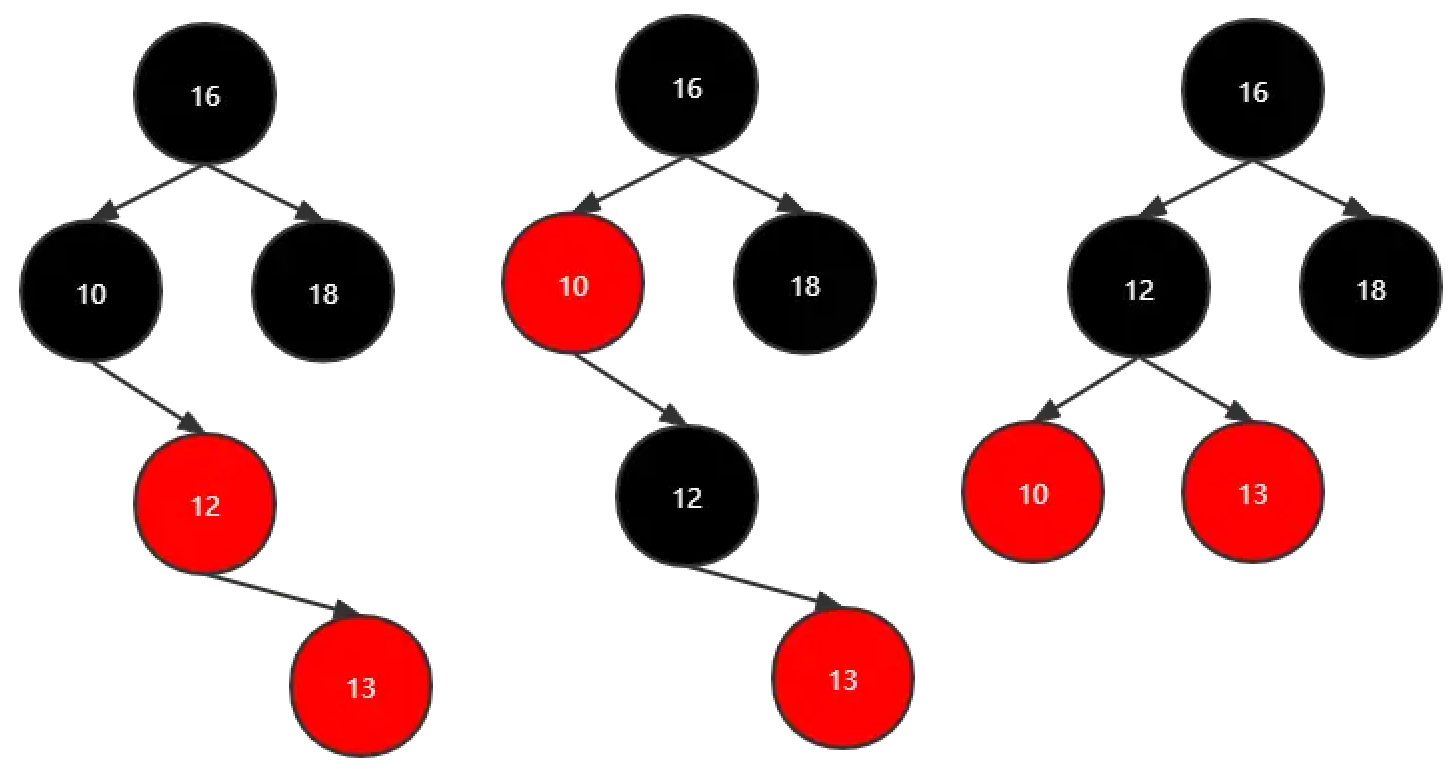
经历三步之后形成新的红黑树
2.插入之后形成LR或者RL
- 先将待插入节点进行旋转,使其变成交换父亲和孩子的关系,使其变成LL或者RR
- 直接将父亲节点变成黑色
- 爷爷节点变成红色
- 进行旋转,以父亲节点的黑色为根节点形成小红黑树插入到大红黑树
总结:先将LR或者RL变成RR或者LL之后再进行调整
向树中插入16:
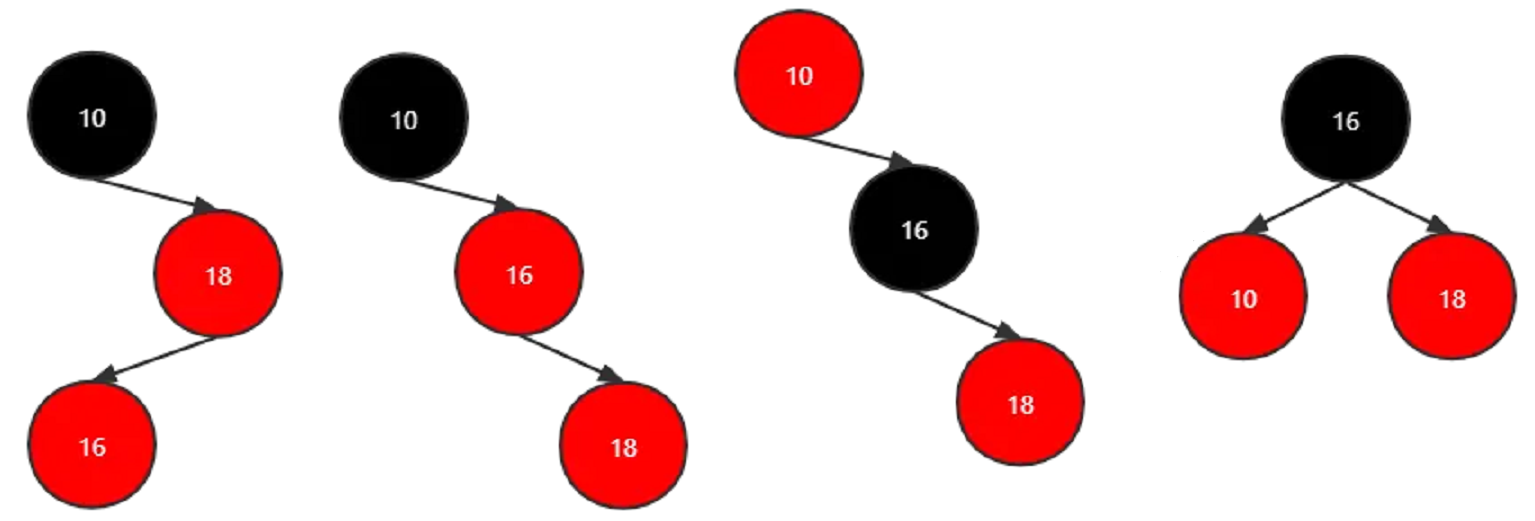
经历四步形成新的红黑树
插入总结
向红黑树中插入节点,主要是当插入位置的父亲节点是红色时比较麻烦,红色又分为两种情况:
- 叔叔节点是红色,此时父亲和叔叔一起变成黑色,爷爷变成红色,就这样一直红黑交替的向上变化,一直到根节点,之后再借鉴平衡二叉树的思想调整
- 叔叔节点是黑色,又分为两种情况
- LL或者RR,此时直接进行变色再旋转:父亲变色、爷爷变色、旋转
- LR或者RL,此时先变成LL或者RR,然后再变色和旋转:旋转、父亲变色、爷爷变色、旋转
删除
红黑树的删除相比于插入来说情况更多,插入总结来说只有四种情况,并且只有插入位置的父节点是红色的情况才略显复杂。
而删除一共有六种组合,待删除节点有2种颜色:红和黑。待删除结点的孩子节点有三种情况:无孩子,一个孩子,两个孩子。所以共有6种情况,下面逐一分析:
组合1:红节点无孩子
这种情况最简单,删除无孩子的红色节点,不影响红黑树中黑色节点的数量
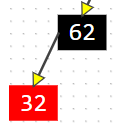
组合2:黑节点无孩子
😄下文详细分析
组合3:红节点一个孩子
这种情况不可能出现,因为一旦出现,当前节点到叶子节点的黑色节点数就不一样,不满足性质5
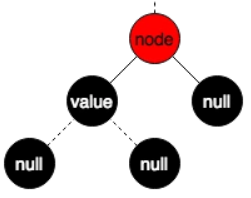
组合4:黑节点一个孩子
此时黑节点的这个孩子节点一定是红色节点,如果是黑色节点的话,左右两边到叶子节点的黑色节点的数量就不相同,有孩子的一边黑色节点数为2,无孩子的一边黑色节点数为1,不满足性质5,所以只能是如图的情况:
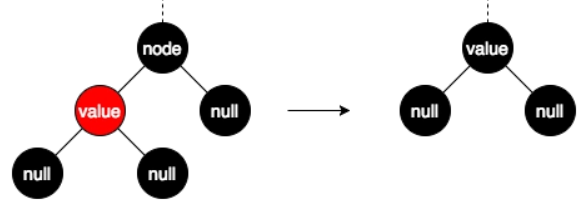
此时只需要将当前节点替换成孩子节点,然后孩子节点变成黑色即可
组合5&6:待删节点有两个孩子
此时不用考虑待删节点的颜色,而是将待删节点用中序遍历的后继节点代替,之后删除这个后继节点即可,但是后继节点的位置不同又会出现不同的情况
- 后继节点没有孩子节点
- 后继节点有一个左孩子
不可能出现后继节点有一个右孩子,如果有的话当前节点就不可能是后继节点
第一种情况,后继节点没有孩子节点,可以转化为组合1或者组合2
当后继节点为红色时,转化为组合1
当后继节点为黑色时,转化为组合2
第二种情况,后继节点有一个左孩子,此时只能转化为组合4,组合3是不可能的
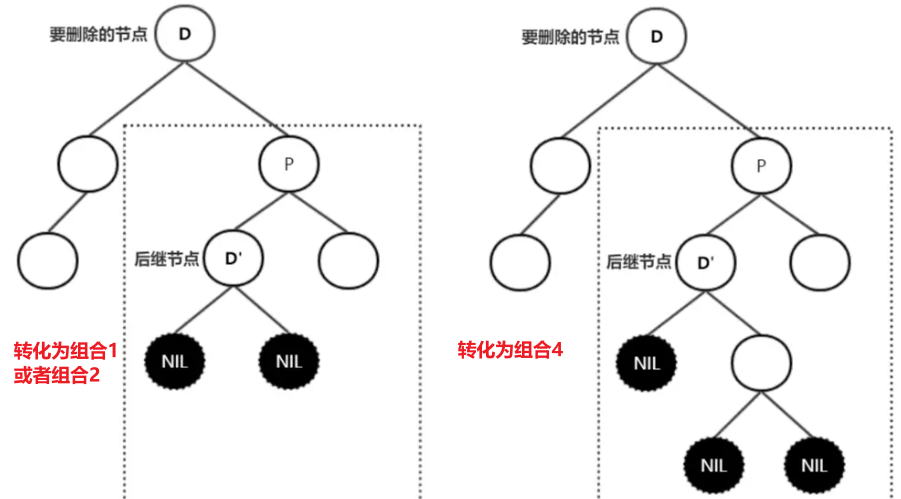
小总结
除了组合2删除单独的黑色节点需要详细分析,剩下的组合5&6转化为了组合1、组合2、组合4,而组合1直接删除,组合4只需要用孩子替换当前节点并变色即可,最复杂的就是组合2:黑节点无孩子,因为删除黑色节点会打乱红黑树的平衡
详解组合2
由于当前节点删除后,相当于变成了一个空节点,红黑树中的空节点是黑色节点,所以这里我们也用黑色空节点代替删除的节点,之后的工作就是调整红黑树使其平衡
情形一:兄弟节点为黑色,且有红色儿子(当前节点的侄子),可分为方向一致和方向不一致
此时删除当前节点node,从node的父节点算起,被删除一侧的黑色节点数与兄弟节点一侧的黑色节点树相比少1,造成了不平衡
进行如下操作:
- 红儿子任选一个,加上brother,father,三个节点形成平衡二叉树
- 叶子节点变成黑色
- 插入到现有红黑树,看根节点涂什么颜色合适
此时将三个节点(孩子节点任选一个)提取出来当作平衡二叉树,最小的放左边,最大的放右边,中间的当根节点,之后在插入红黑树中,进行染色
总结:删除之后剩下三个节点:father,brother,nephew,将这三个节点先变成平衡二叉树,在编程红黑树
son与brother方向一致(L或者RR),直接旋转:
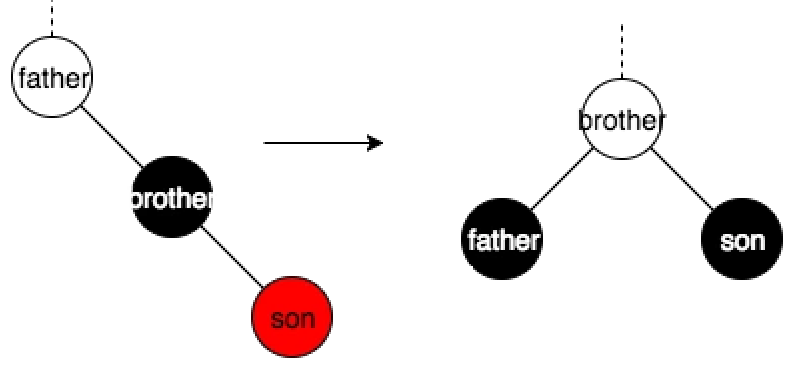
son与father方向不一致,LR、RL变成LL或RR:
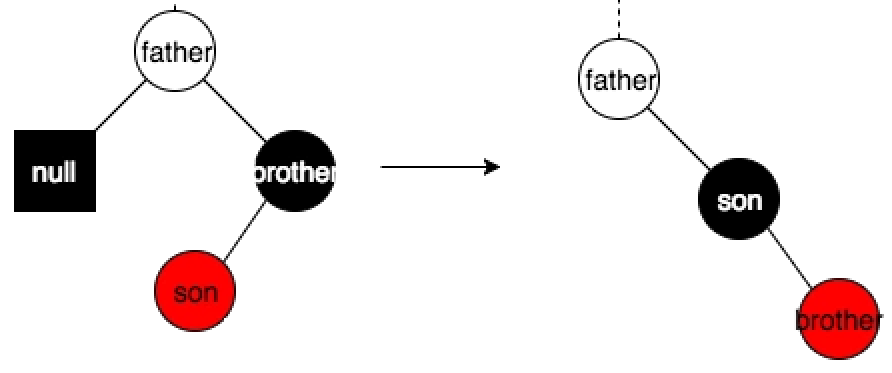
变成LL或RR之后在进行旋转
情形二:兄弟节点为黑色,没有儿子
红黑树不平衡的情况是因为被删除的一侧少了一个黑色节点,而兄弟节点是黑色的,所以出现不平衡,此时需要减少兄弟一侧的黑色节点数,解决办法就是将兄弟变成红色,分为两种情况:
父节点为红色,兄弟节点直接变成红色之后,父节点变成黑色,此时不论父节点的父节点是什么颜色,只会出现两种情况,黑黑或者红黑,都满足红黑树的性质
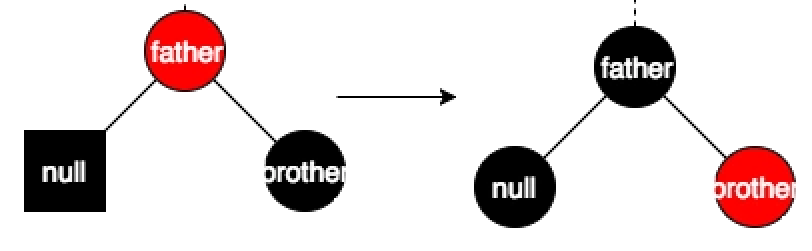
也就是父节点和兄弟节点变化颜色即可
父节点为黑色
情形三:兄弟节点为红色
此时兄弟节点是红色,当前节点是黑色,父节点只能是黑色
进行如下操作:
brother旋转当根节点,当前节点变成游离节点father变成红色,brother变成黑色(根节点)其余节点颜色不变,参考二叉排序树插入剩下节点游离节点的删除变成上面的任意一种情况
删除总结
删除分为六种组合,其中组合3不可能出现,剩下五种组合,组合5&6可以转化为组合1,2,4.而组合1、4又比较简单。所以只剩下了组合2.
对于组合2来说,待删除节点固定为黑色,兄弟节点颜色不一样并且孩子节点的分布也不一样,所以又需要划分情况:
兄弟节点为黑色,孩子节点与兄弟节点方向一致
兄弟节点为黑色,孩子节点与兄弟节点方向不一致
兄弟节点为黑色,无孩子节点
- 父节点为红色
- 父节点为黑色(未解决😤😤😤)
兄弟节点为红色,此时父节点一定为黑色(未解决😤😤😤)
总结
平衡二叉树的插入就是先插入,然后调整,调整的思路就是找到最小不平衡子树到插入节点的一条路径,然后取出前三个节点形成一个平衡二叉树,剩下的元素在不改变父子和兄弟关系的前提下逐一插入二叉树即可
平衡二叉树的删除就是先进行二叉搜索树的删除,之后借鉴平衡二叉树插入的思想进行调整,直到平衡,可能会调整多次
红黑树的插入中一共有四种情况,最麻烦的就是插入位置的父节点为红色,因为默认插入的新节点为红色,所以需要进行调整,根据叔叔节点的颜色又分为不同的情况,叔叔节点为红色时,父亲和叔叔一起从红变黑,爷爷节点从黑变红,一层一层向上,直到根节点,之后再借鉴平衡二叉树的思想进行调整。叔叔节点为黑色(空节点),只需要将当前节点,父亲节点,爷爷节点三个形成一个红黑树,插入原有红黑树即可。
红黑树的删除一共有六种情况,除了组合3不可能,组合5&6可转化为组合1、2、4。剩下的组合1、2、4中最麻烦的就是组合2。
组合2分为兄弟节点为黑色(又分为三种情况)和兄弟节点为红色。
还剩下几种情况未解决。。。。。。😂😂😂